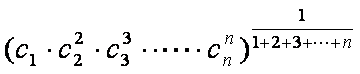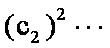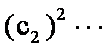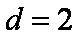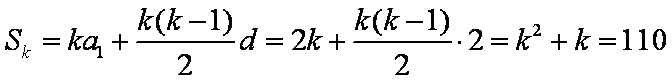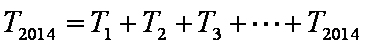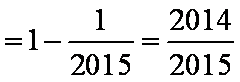- 由数列的前几项求通项
- 共480题
9.对于实数m,n定义运算“⊕”:m⊕n=
正确答案
解析
略。
知识点
11. 已知数列



正确答案
26
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列





(1)求证:数列
(2) 设





正确答案
见解析。
解析
(Ⅰ) 由题设


当

两式相减得
方法一:由


则数列


所以数列


方法二:由

两式相减得

所以数列
(Ⅱ) 由(Ⅰ)得


当

当

所以
综上所述,命题得证. ………………………………14分
知识点
10.对于一个有限数列p=(p1,p2,…,pn),p的蔡查罗和(蔡查罗是一位数学家)定义为
正确答案
解析
略。
知识点
16.观察下列等式:
①sin2θ=cosθ•2sinθ
②sin4θ=cosθ(4sinθ﹣8sin3θ)
③sin6θ=cosθ(6sinθ﹣32sin3θ+32sin5θ)
④sin8θ=cosθ(8sinθ﹣80sin3θ+192sin5θ﹣128sin7θ)
⑤sin10θ=cosθ(10sinθ﹣160sin3θ+msin5θ﹣1024sin7θ+nsin9θ)
则可以推测(1)n=________;(2)m=________。
正确答案
(1)n=512
(2)m=672
解析
略。
知识点
17.对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出定义:设f′(x)是函数y=f(x)的导数,f′′(x)是f′(x)的导数,若方程f′′(x)有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数f(x)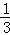
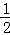

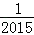
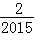

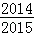
正确答案
2014
解析
略。
知识点
19.数列{an}中,已知a1=1,n≥2时,an=
(1)求证:数列{bn}是等差数列;
(2)求数列{an}的前n项和Sn。
正确答案
见解析。
解析
(1)证明:由
得:
∴
即bn=bn﹣1+2⇒bn﹣bn﹣1=2(n≥2)
又
∴数列{bn}是首项为2,公差为2的等差数列。
(2)解:由(1)知,bn=2+(n﹣1)×2=2n,
∴
记
则
两式相减得:
=
∴
因此,
知识点
15.已知数列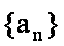
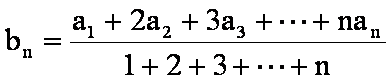
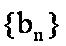
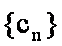
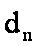
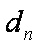
正确答案
解析
由等差数列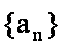
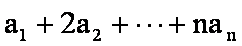
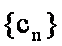
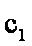
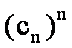
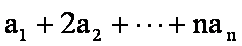
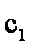
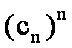

知识点
18.设等差数列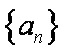
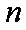
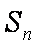
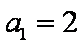
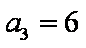
(1)求数列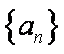
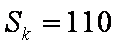
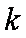
(3)设数列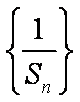
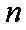
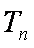
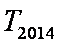
正确答案
见解析。
解析
(1)设等差数列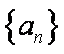
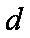
∵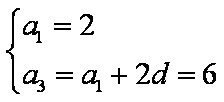
∴
数列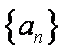
(2)方法一:∵
解得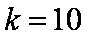
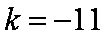
方法二:∵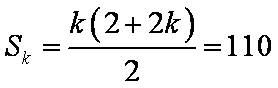
解得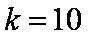
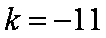
(3)∵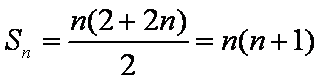

∴
知识点
20.已知首项为
(1)求数列{an}的通项公式;
(2)证明
正确答案
见解析
解析
(1)设等比数列{an}的公比为q,因为-2S2,S3,4S4成等差数列,
所以S3+2S2=4S4-S3,即S4-S3=S2-S4,
可得2a4=-a3,于是
又a1=

(2)证明:
当n为奇数时,

当n为偶数时,

故对于n∈N*,有
知识点
扫码查看完整答案与解析