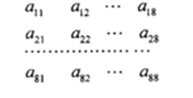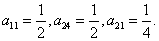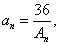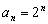- 由数列的前几项求通项
- 共480题
已知等差数列





(1)求数列
(2)求数列

正确答案
(1)
(2)
解析
(1)因为
所以
因为
所以
由①,②及

所以
(2)由

所以 
所以

所以 数列


知识点
已知m是两个正数2和8的等比中项,则圆锥曲线

正确答案
解析
略
知识点
已知等差数列


(1)求数列
(2)若数列





正确答案
见解析。
解析
(1)设数列

解得:

(2) 




知识点
64个正数排成8行8列,如右图所示:
其中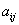
(1)求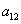
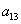
(2)记第n行各项之和为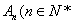
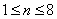
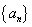
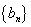
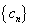
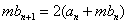
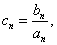
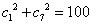
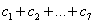
(3)对(2)中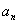
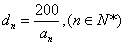
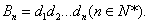
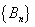
正确答案
见解析。
解析
(1)因为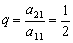
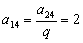
又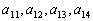
所以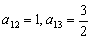
(2)由(1)得,第一行所成等差数列公差为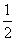
所以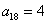
因为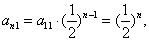
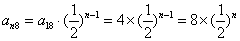
所以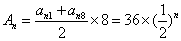
所以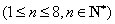
因为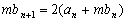
所以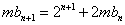
整理得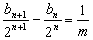
而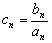
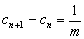
所以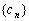
故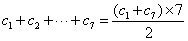
因为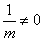
所以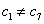
所以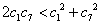
所以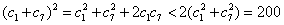
所以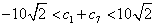
所以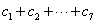
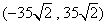
(3)因为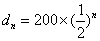
所以当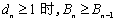
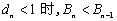
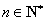
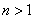
所以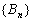
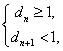
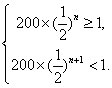
解得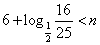
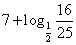
又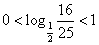
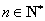
所以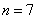
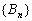
知识点
若①


正确答案
25
解析
略
知识点
扫码查看完整答案与解析