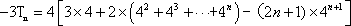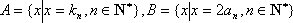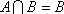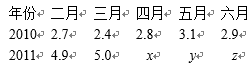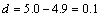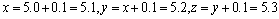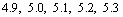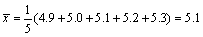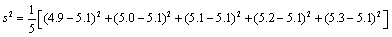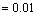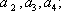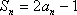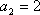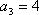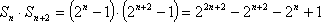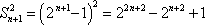- 由数列的前几项求通项
- 共480题
已知数列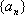

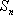

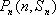
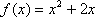
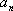
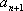
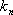
(1)求数列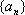
(2)若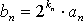


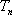
(3)设集合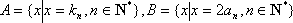
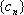
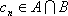
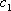
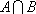
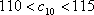
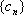
正确答案
见解析
解析
(1)
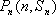
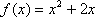
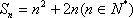
当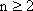
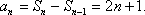
当n=1时,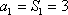
所以数列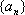
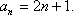
(2)∵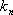
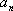
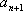
∴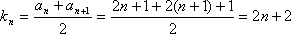
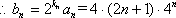
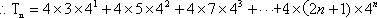
由①×4,得
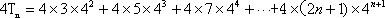
①-②得:
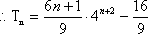
(3)∵
∴
∵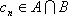
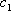
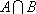
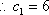
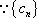
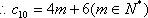
又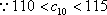
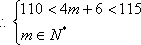
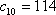
设等差数列的公差为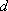
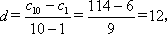
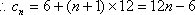
∴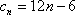
知识点
某校高二年级研究性学习小组,为了分析2011年我国宏观经济形势,上网查阅了2010年和2011年2—6月我国CPI同比(即当年某月与前一年同月相比)的增长数据(见下表),但2011年4,5,6三个月的数据(分别记为x,y,z)没有查到. 有的同学清楚记得2011年2,3,4,5,6五个月的CPI数据成等差数列.
(1)求x,y,z的值;
(2)求2011年2—6月我国CPI的数据的方差;
(3)一般认为,某月CPI达到或超过3个百分点就已经通货膨胀,而达到或超过5个百分点则严重通货膨胀. 现随机地从上表2010年的五个月和2011年的五个月的数据中各抽取一个数据,求相同月份2010年通货膨胀,并且2011年严重通货膨胀的概率.
附表:我国2010年和2011年2~6月的CPI数据(单位:百分点. 注:1个百分点=1%)
正确答案
见解析。
解析
(1)依题意得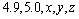
故
(2)由(1)知2011年2~6月我国CPI的数据为:
其平均数为:
其方差为:
(3)用(m,n)表示随机地从2010年的五个月和2011年的五个月的数据中各抽取一个数据的基本事件,其中m表示2010年的数据,n表示2011年的数据,则所有基本事件有:
(2.7,4.9),(2.7,5.0),(2.7,5.1),(2.7,5.2),(2.7,5.3),(2.4,4.9),(2.4,5.0),(2.4,5.1),(2.4,5.2),(2.4,5.3),(2.8,4.9),(2.8,5.0),(2.8,5.1),(2.8,5.2),(2.8,5.3),(3.1,4.9),(3.1,5.0),(3.1,5.1),(3.1,5.2),(3.1,5.3),(2.9,4.9),(2.9,5.0),(2.9,5.1),(2.9,5.2),(2.9,5.3);共25种.
其中满足相同月份2010年通货膨胀,并且2011年严重通货膨胀的基本事件有:
(3.1,5.0),(3.1,5.1),(3.1,5.2),(3.1,5.3),共4种,
所以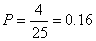
知识点
设集合

①
②存在实数


(1)


中属于集合W的数列编号为 ( )
正确答案
解析
略
知识点
数列{




(1)求数列{
(2)设


正确答案
见解析。
解析
(1)由点



当



当

∴数列{
(2)由
∴
上式两边乘以2,得
① -②得
∴

知识点
数列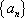
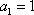

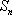
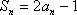
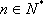
(1)求出
(2)求数列
(3)求证: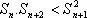
正确答案
见解析
解析
(1)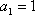
∴当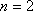
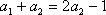

当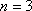

当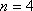
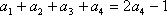
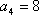
(2)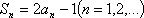
∴
(1)-(2)得 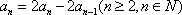
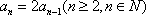
所以数列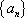
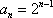
(3)证明: 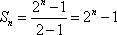
∴
∴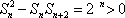
∴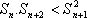
知识点
扫码查看完整答案与解析