- 由数列的前几项求通项
- 共480题
已知等比数列



正确答案
解析
略
知识点
数列{an}的前n项和为Sn=2an﹣2,数列{bn}是首项为a1,公差不为零的等差数列,且b1,b3,b11成等比数列。
(1)求a1,a2,a3的值;
(2)求数列{an}与{bn}的通项公式;
(3)求证:
正确答案
见解析。
解析
解:(1)∵Sn=2an﹣2,
∴当=1时,a1=2a1﹣2,解得a1=2;
当n=2时,S2=2+a2=2a2﹣2,解得a2=4;
当n=3时,s3=a1+a2+a3=2a3﹣2,解得a3=8.
(2)当n≥2时,an=sn﹣sn﹣1=2an﹣2﹣(2an﹣1﹣2)=2an﹣2an﹣1
得an=2an﹣1又,a1=2,
∴数列{an}是以2为首项,公比为2的等比数列,
所以数列{an}的通项公式为
b1=a1=2,设公差为d,则由且b1,b3,b11成等比数列
得(2+2d)2=2(2+10d),
解得d=0(舍去)或d=3,
∴bn=3n﹣1.
(3)令Tn=
=
∴2Tn=
两式式相减得
=5﹣
又

知识点
已知数列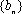
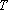
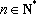
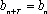
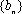
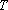
数列



数列
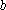

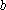
数列
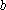


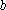

(1)对于数列②,它的一个通项公式可以是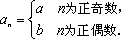
(2)求数列③的前
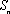
(3)在数列③中,若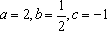
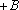
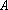
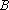

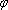
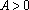
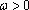
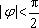
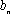
正确答案
见解析
解析
(1)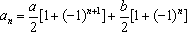
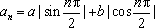
(2)当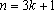
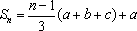
当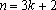
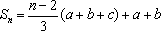
当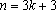
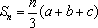
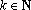
(3)由题意,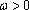
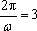
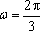
于是
把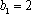
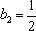
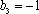
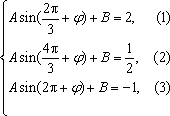
由(1)(2)可得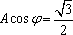
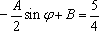
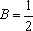
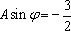
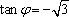
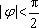
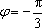
于是可求得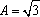
故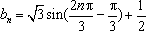
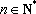
或写成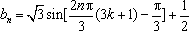
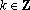
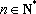
知识点
设定义在









正确答案
5,10
解析
略
知识点
已知数列




(1)求数列
(2)在







(3)记





正确答案
见解析
解析
解析:(1)当


当



即



所以,

(2)由题意,


因为



所以



所以这个等差数列所有项的和
所以,

(3)由(1)知

由题意,


所以

因为



所以



所以,当

知识点
扫码查看完整答案与解析