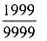由数列的前几项求通项
共480题

· 由数列的前几项求通项

由数列的前几项求通项
共480题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 4 分

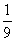
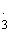
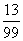
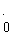
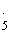
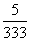
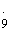
无限循环小数可以化为分数，如0.i=，0.i=,0.1=，…，请你归纳出0.99=________；

正确答案

解析

略

知识点

由数列的前几项求通项

题型：简答题

简答题 · 12 分

已知数列满足.

（1）求数列的通项公式；

（2）设，求数列的前n项和.

正确答案

见解析。

解析

知识点

由数列的前几项求通项

题型：填空题

填空题 · 4 分

若函数的解集是

正确答案

解析

略

知识点

由数列的前几项求通项

题型：简答题

简答题 · 12 分

设是首项为,公差为的等差数列,是其前项和。

（1）若，求数列的通项公式；

（2）记,，且成等比数列,证明:().

正确答案

见解析。

解析

（1）因为是等差数列，由性质知，…………2分

所以是方程的两个实数根，解得，………4分

∴或

即或.……………6分

（2）证明:由题意知∴ ∴ …………7分∵成等比数列，∴ ∴ …………8分∴ ∴ ∵ ∴ ∴…10分 ∴ ∴左边= 右边= ∴左边=右边∴()成立. ……………12分

知识点

由数列的前几项求通项

题型：简答题

简答题 · 13 分

对于无穷数列，记，给出下列定义：①若存在实数，使成立，则称数列为“有上界数列”；②若为有上界数列，且存在，使成立，则称为“有最大值数列”；③若，则称数列为“差减小数列”。

（1）根据上述定义，判断数列，分别是那种数列？

（2）在数列中，，，求证：数列既是有上界数列又是差减小数列；

（3）若数列是有上界数列且是差减小数列但不是有最大值数列，求证：无穷数列为单调递增数列。

正确答案

见解析

解析

（1）1），显然，且存在，，

，

所以数列既是由上界数列，又是有最大值数列， ………2分

2），,,,

且不存在，使成立；所以数列是差减小数列，又是有上界数列 …4分

（2）下面用反证法证明，假设存在某个k使得，成立，则必有，显然与已知矛盾，所以不成立；假设存在某个k使得，成立，则必有成立，即得到成立，与矛盾，所以。

又 , ，两式相减得：,即,即,所以既是差减少数列又是有上界数列，………4分

（3）用反证法，假设无穷数列不是单调递增数列，则设k为第一个使成立的自然数，即，又是差减小数列，所以即，数列从第k项开始都有，即，又因为此时，所以数列从第k项开始为单调递减数列，又由于k为第一个使成立的自然数，所以无穷数列中，必有，

无穷数列为有最大值数列，与已知矛盾，所以假设不成立，无穷数列一定是单调递增数列，5分

知识点

由数列的前几项求通项

继续学习学习下一知识点

下一知识点 : 由an与Sn的关系求通项an

百度题库 > 高考 > 文科数学 > 由数列的前几项求通项

扫码查看完整答案与解析