- 二次函数的应用
- 共461题
1
题型:
单选题
|
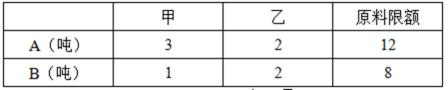
8.某企业生产甲乙两种产品均需用A,B两种原料,已知生产1吨每种产品需原料及每天原料的可用限额如表所示,如果生产1吨甲、乙产品
正确答案
D
解析
设每天生产甲乙两种产品分别为x,y顿,利润为z元,
则3x+2y≤12x+2y≤8x≥0,y≥0, 目标函数为 z=3x+4y.
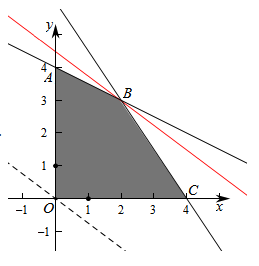
作出二元一次不等式组所表示的平面区域(阴影部分)即可行域。
由z=3, 即B的坐标为x=2,y=3,
∴Zmax=3x+4y=6+12=18.
即每天生产甲乙两种产品分别为2,3顿,能够产生最大的利润,最大的利润是18万元,
考查方向
本题主要考查应用题、线性规划最优解等知识,意在考查考生的理解问题解决问题的能力和数形结合的能力.
解题思路
设每天生产甲乙两=3x+4y得y=-34x+z4,
平移直线y=-34x+z4由图象可知当直线y=-34x+z4经过点B时,直线y=-34x+z4的截距最大, 此时z最大,
解方程组3x+2y=12x+2y=8,解得x=2y=分别为x,y顿,利润为z元,然后根据题目条件建立约束条件,得到目标函数,画出约束条件所表示的区域,然后利用平移法求出z的最大值.
易错点
1.不会根据题意设变量表示题中的约束条件;
2.不会利用线性规划求目标函数的最值。
教师点评
考生需要掌握目标函数的设立,了解约束条件并作图标,利用线性规划求目标函数的最值。
知识点
二次函数的应用根据实际问题选择函数类型
下一知识点 : 幂函数的概念、解析式、定义域、值域
扫码查看完整答案与解析