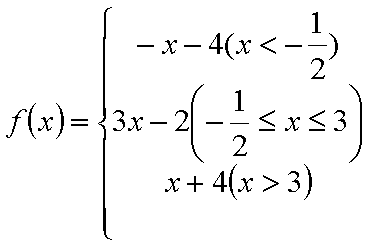- 不等式选讲
- 共57题
14.已知实数x,y满足
正确答案
15
解析
试题分析:由直线与圆的位置关系,去掉绝对值,利用线性规划求出最大值。
由

要使z=-3x-4y+10最大,则直线
由z=-3x-4y+10,得3x+4y+z-10=0.
则
故答案为:15.
考查方向
解题思路
由题意可得2x+y-4<0,6-x-3y>0,去绝对值后得到目标函数z=﹣3x﹣4y+10,然后结合圆心到直线的距离求得|2x+y-4|+|6-x-3y |的最大值.
易错点
根据直线与圆的位置关系来判断绝对值内数值的正负.
知识点
24.已知函数f(x)=| x+1| -|2x-3|.
(Ⅰ)在答题卡第24题图中画出y=f(x)的图像;
(Ⅱ)求不等式| f(x)|>1的解集.
正确答案
1
知识点
17.已知函数
(1)证明:
(2)求不等式:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
选修4-1:几何证明选讲
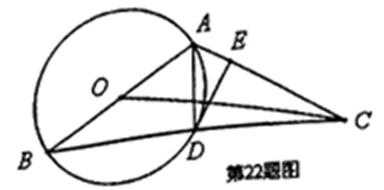
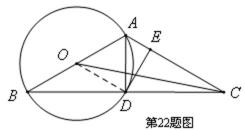
如图,以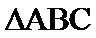
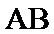
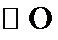
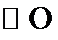
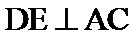
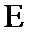
27.求证:
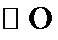
28.若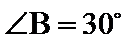
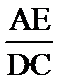
正确答案
详见解析
解析
(Ⅰ)如图,连接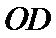
因为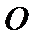
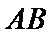
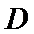
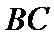
所以 
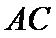
因为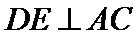
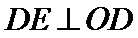
所以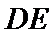
考查方向
圆的切线的性质和判断
解题思路
连接OD,根据垂直关系证明DE是圆O的切线
易错点
不能作出正确的辅助线,找不到垂直关系
正确答案
详见解析
解析
(Ⅱ)因为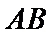
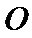
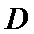
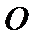

又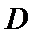
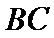
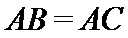
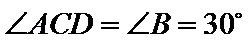
因为
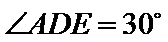
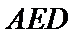
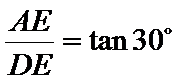
在直角三角形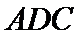
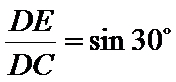
于是
考查方向
与圆有关的比例线段
相似三角形的性质和判定
解题思路
根据直角三角形中的比例线段,求出答案
易错点
找不到相似条件,不能求出正确的答案
已知集合


正确答案
解析
略
知识点
设

正确答案
解析
略
知识点
若

正确答案
解析
略。
知识点
由



(1)若

(2)求证:
(3)求
(注:对任意

正确答案
见解析
解析
(1)
(2)证明:由
=
(3)



其中最大数之和与最小数之和的差为

对于

所以

注:使得
知识点
设函数
(1) 求函数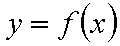
(2) 若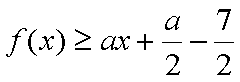
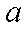
正确答案
见解析
解析
(1)由题意得
所以 f(x)在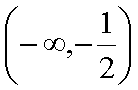
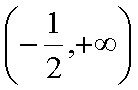
所以当
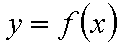
此时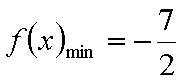
(2)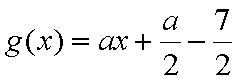
由图象可知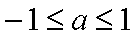
知识点
21.已知函数

(1)证明:

(2)若关于



(3)已知正数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析