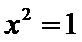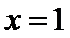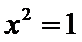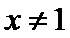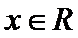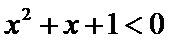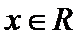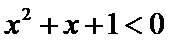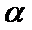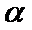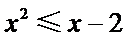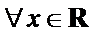简单的逻辑联结词、全称量词与存在量词
共96题

简单的逻辑联结词、全称量词与存在量词
共96题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

4.命题“且f(n)≤n的否定形式是（）

A且f(n)＞n

B或f(n)＞n

C且

D或

正确答案

解析

试题分析：由全称命题的否定是特称命题，得出结论即可。

“且f(n)≤n的否定形式是：“或 ”，

故选D.

考查方向

本题考查了含有量词的命题的否定，属于基础题．

解题思路

根据全称命题的否定，把任意改为存在，然后否定结论即可．

易错点

注意含有量词的命题的否定中把任意改为存在，且的否定为或.

知识点

全（特）称命题的否定

题型：单选题

单选题 · 5 分

3．给定下列两个命题：

①“p∨q”为真是“¬p”为假的必要不充分条件；

②“xR，使sinx＞0”的否定是“xR，使sinx0”．

其中说法正确的是( )

A①真②假

B①假②真

C①和②都为真

D①和②都为假

正确答案

解析

对于命题1，由¬p为假可以推出p∨q为真，但由p∨q为真不能推出¬p为假的值，所以前者是后者的必要不充分条件，命题1正确。易得命题2也是正确的。所以选C

考查方向

命题真假的判断；充分条件；必要条件

解题思路

根据相关性质，逐一判断

易错点

对逻辑与命题理解不透彻；

知识点

含有逻辑联结词命题的真假判断全（特）称命题的否定

题型：单选题

单选题 · 5 分

4.下列结论正确的是（）

A命题“若，则”的否命题为：“若，则”

B已知是R上的可导函数，则“”是“是函数的极值点”的必要不充分条件

C命题“存在，使得”的否定是：“对任意，均有”

DD.命题“角的终边在第一象限角，则是锐角”的逆否命题为真命题

正确答案

解析

根据否命题是条件结论全否，所以A错。

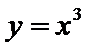
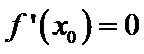
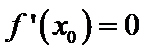
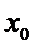
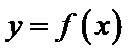
特例中不是函数的极值点，所以则“”是“是函数的极值点”的必要不充分条件正确所以选B

特称命题的否定是全称命题，且否定结论，所以C错

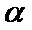
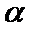
命题“角的终边在第一象限角，则是锐角”是假命题，所以逆否命题为假命题，所以D错所以选B

考查方向

本题主要考察了四种命题及真假判断，导函数的性质，命题的否定，命题的真假判断与应用，充分，必要条件的判定，全（特）称命题的否定，属于基本概念题，使用排除法

解题思路

1）否命题是条件结论全否，命题的否定是只否定结论，对A C D进行选择

2）使用充分，必要条件的判定对BC进行排除

易错点

本题易错于否命题和命题的否定的区别，导致无法排除

知识点

含有逻辑联结词命题的真假判断全（特）称命题的否定

题型：单选题

单选题 · 5 分

5. 下列有关命题说法正确的是（）

A命题p：“”，则p是真命题

B的必要不充分条件

C命题的否定是：“”

D“”是“上为增函数”的充要条件

正确答案

解析

对于A选项，，所以命题p是真命题，所以p是假命题，故A选项错误；对于B选项，由解得或，所以的充分不必要条件，故B错误；对于C选项，命题的否定是：“”，故C错误；对于D选项，上为增函数”则，所以D选项正确，所以选D。

考查方向

本题主要考查简易逻辑部分的知识，意在考查考生的逻辑推理能力。

解题思路

逐个选项判断正误即可。

易错点

1.不明白充分必要条件误选B；2.对于D选项中的对数函数的增减性弄错导致出错。

知识点

含有逻辑联结词命题的真假判断全（特）称命题的否定

题型：单选题

单选题 · 5 分

3．下列命题中，真命题是

A，

B，

C函数为定义域上的减函数

D“被2整除的整数都是偶数”的否定是“至少存在一个被2整除的整数不是偶数”

正确答案

解析

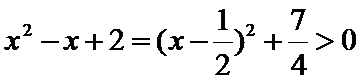
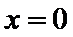
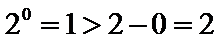
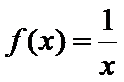
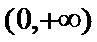
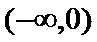
因为恒成立，即选项A错误；当时，不成立，即选项B错误；因为函数在，上单调递增，但单调区间不能加并集，即选项C错误；“被2整除的整数都是偶数”的否定是“至少存在一个被2整除的整数不是偶数”，即选项D正确；所以选D选项.

考查方向

本题以命题真假的判定为载体主要考查了全称命题、特称命题、命题的否定、函数的单调性，在近几年的各省高考题中出现的频率较高，常与代数、几何、三角函数等知识交汇命题.

解题思路

1)分别判断各选项的真假；

2)得出答案.

易错点

本题易在判断选项C时出现错误，易忽视“单调区间之间不能加并集符号”.

知识点

含有逻辑联结词命题的真假判断全（特）称命题的否定

题型：单选题

单选题 · 5 分

2．命题“≤0，使得≥0”的否定是

A≤0，＜0

B≤0，≥0

C＞0，＞0

D＜0，≤0

正确答案

解析

根据全（特）称命题的否定：存在性命题的否定是全称命题，排除CD，再根据语句要否定，排除B，选择A

考查方向

本题主要考察了全（特）称命题的否定，属于基本概念题

解题思路

根据存在性命题的否定直接得出结果

易错点

本题易错于全（特）称命题的否定的形式，导致无法排除

知识点

含有逻辑联结词命题的真假判断全（特）称命题的否定

已学完, 返回章节学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 简单的逻辑联结词、全称量词与存在量词

扫码查看完整答案与解析