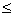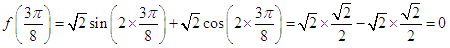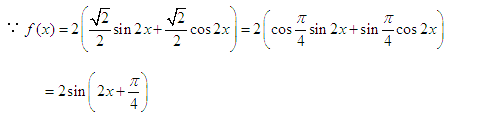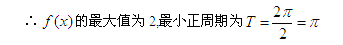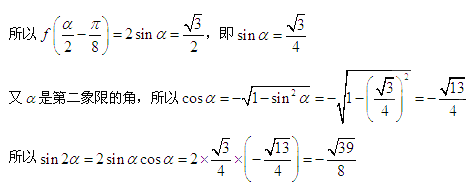- 三角函数的最值
- 共55题
已知函数f(x)=(2cos2x-1)sin 2x+
(1)求f(x)的最小正周期及最大值;
(2)若α∈

正确答案
(1)f(x)的最小正周期为

(2)
解析
(1)因为f(x)=(2cos2x-1)sin 2x+
=cos 2xsin 2x+
=
=
所以f(x)的最小正周期为

(2)因为f(α)=

因为α∈


所以

知识点
设函数f(x)=sinxcosx-cos(x+π)cosx(x∈R)。
(1)求f(x)的最小正周期;
(2)若函数y=f(x)的图象按b=平移后得到函数y=g(x)的图象,求y=g(x)在上的最大值。
正确答案
见解析。
解析
知识点
已知

(1)求函数
(2)求函数
正确答案
见解析。
解析
(1)


此时


(2)由

所以函数

知识点
函数
正确答案
解析
因为








知识点
已知向量

(1) 求f (x)的最小正周期.
(2)求f (x) 在
正确答案
见解析
解析
(1) 

最小正周期
所以

(2)

所以,f (x) 在

知识点
函数f(x)=sin(x+φ)﹣2sinφcosx的最大值为 1 。
正确答案
1
解析
∵f(x)=sin(x+φ)﹣2sinφcosx=sinxcosφ+cosxsinφ﹣2sinφcosx=sinxcosφ﹣sinφcosx=sin(x﹣φ)。
∴f(x)的最大值为1
知识点
已知函数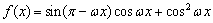
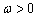
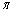
(1)求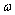
(2)将函数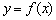

函数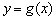
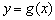
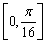
正确答案
见解析。
解析
因此 1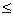
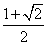
知识点
已知函数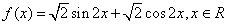
(1)求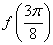
(2)求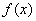
(3)若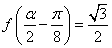
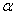
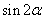
正确答案
见解析。
解析
(1)
(2)
(3)
由(2)可知
知识点
已知函数

(1)求
(2)已知



正确答案
见解析
解析
(1)




(2)证明:由已知得
两式相加得



∴
知识点
正确答案
见解析。
解析
知识点
扫码查看完整答案与解析