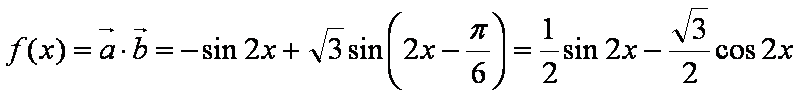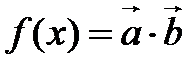- 三角函数的最值
- 共55题
函数
(1)求函数
(2)求函数


正确答案
见解析
解析
解(1)由图知
∴


∵


∴

∵


(2)由
解得函数

函数

知识点
设函数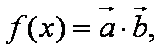
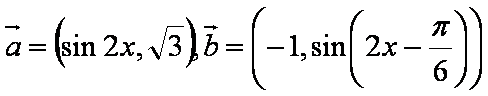
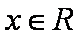
(1)求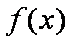
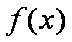
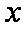
(2)将函数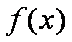
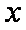
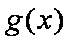
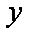
正确答案
见解析。
解析
(1)
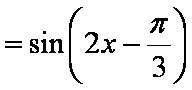
故函数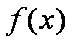
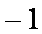
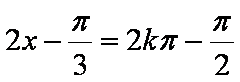
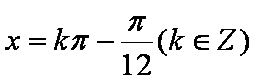
故使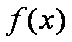
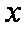
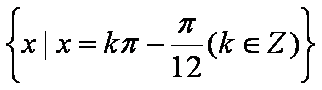
(2)由条件可得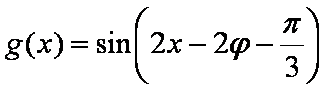
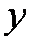
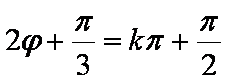
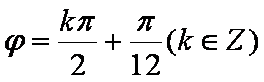
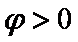
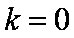
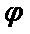
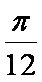
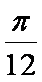
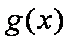
知识点
16.已知向量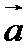
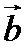
(1)求f (x)的最小正周期;
(2)求f(x)在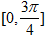
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.将函数


(1)求
(2)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设函数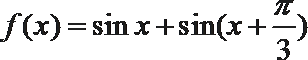
(1)求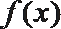
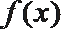
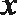
(2)不画图,说明函数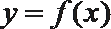
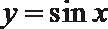
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知:函数



(1)求:
(2)当

正确答案
(1)由最高点为


由点

所以
又


(2)因为
所以当
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求
(2)将




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求函数
(2)求函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.向量
(I)若a为任意实数,求g(x)的最小正周期;
(II)若g(x)在[o,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析