三角函数的最值
共55题

· 三角函数的最值

三角函数的最值
共55题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

18．中，分别为角的对边，满足.

（Ⅰ）求角的值；

（Ⅱ）若，设角的大小为的周长为，求的最大值.

正确答案

（Ⅰ）在中，由及余弦定理得

而，则；

（Ⅱ）由及正弦定理得，

同理

∴

∵∴，

∴即时，．

解析

解析已在路上飞奔，马上就到！

知识点

正弦定理余弦定理三角函数的最值

题型：简答题

简答题 · 12 分

18．已知函数．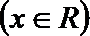

（Ⅰ）若，求的最大值；

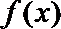
（Ⅱ）求函数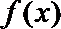的单调区间及对称轴方程；

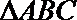
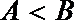
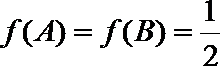
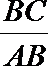
（Ⅲ）在中，若，，求的值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的单调性正弦函数的对称性三角函数中的恒等变换应用正弦定理三角函数的最值

题型：简答题

简答题 · 12 分

17．设向量.

（Ⅰ）若，求的值；

（Ⅱ）设函数，求的最大值.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的化简求值三角函数中的恒等变换应用三角函数的最值向量的模平面向量数量积的运算

题型：简答题

简答题 · 12 分

17．已知函数

（1）求的值；

（2）求的最大值和最小值。

正确答案

（1）（2）

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的化简求值三角函数中的恒等变换应用三角函数的最值

题型：简答题

简答题 · 12 分

17．设函数。

（1）求的最小正周期。

（2）若函数与的图像关于直线对称，求当时的最大值。

正确答案

（1）

．

故的最小正周期为

（2）解法一：在的图象上任取一点，

它关于的对称点

由题设条件，点在的图象上，

从而

当时，，

因此在区间上的最大值为

解法二：因区间关于x = 1的对称区间为，

且与的图象关于x = 1对称，

故在上的最大值就是在上的最大值

由（1）知，

当时，

因此在上的最大值为

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法三角函数中的恒等变换应用三角函数的最值

题型：简答题

简答题 · 12 分

17．已知函数

（I）求函数的最小值和最小值时x的集合；

（II）设△ABC的内角A，B，C对边分别为a，b，c，且与的值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数中的恒等变换应用正弦定理余弦定理三角函数的最值平行向量与共线向量

题型：简答题

简答题 · 12 分

17.设函数的图象经过点．

（Ⅰ）求的解析式，并求函数的最小正周期和最值．

（Ⅱ）若，其中是面积为的锐角的内角，且，求和的长．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法三角函数中的恒等变换应用正弦定理三角函数的最值

题型：单选题

单选题 · 5 分

8. 命题，函数，则（）

A是假命题；，

B是假命题；，

C是真命题；，

D是真命题；，

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的否定命题的真假判断与应用三角函数的最值

题型：简答题

简答题 · 12 分

17．已知向量，，且

（1）求的取值范围；

（2）求函数的最小值，并求此时x的值

正确答案

解析：（1）∵　　　

∴　；　　

∴　0≤≤2　　　　

（2）∵　　　

∴　；

∵　

∴　当，即或时，取最小值－。

解析

解析已在路上飞奔，马上就到！

知识点

三角函数中的恒等变换应用三角函数的最值向量的模平面向量数量积的运算

题型：简答题

简答题 · 12 分

19．已知向量，

（1）当向量与向量共线时，求的值；

（2）求函数的最大值,并求函数取得最大值时的的值.

正确答案

（1）)共线,∴,∴.

（2）,

，

函数的最大值为,

得函数取得最大值时

解析

解析已在路上飞奔，马上就到！

知识点

三角函数中的恒等变换应用三角函数的最值平面向量共线（平行）的坐标表示平面向量数量积的运算

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 文科数学 > 三角函数的最值

扫码查看完整答案与解析