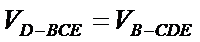- 棱柱、棱锥、棱台的体积
- 共114题
16.三棱柱


正确答案
(16)
知识点
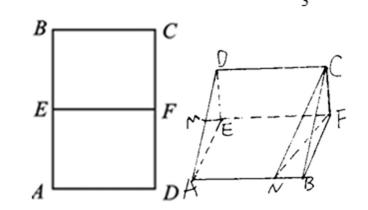
如图甲,在矩形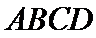
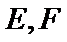
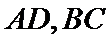
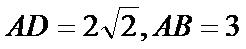
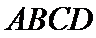
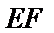
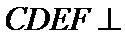
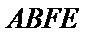

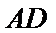

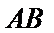
21.证明:
22.若三棱锥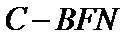
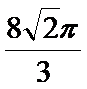

正确答案
(Ⅰ)证明:由已知EF⊥AE,EF⊥DE,
∴EF⊥平面AED.
又AB∥EF,∴AB⊥平面AED,又EM
又在等腰△AED中,M是AD中点,故EM ⊥AD,
∴EM ⊥平面ABCD,又CN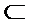
正确答案
(Ⅱ)解:∵三棱锥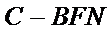
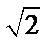
注意到△CFN,△CBN都是直角三角形,CN是斜边,
故球心为CN的中点,即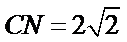
在Rt△CFN中,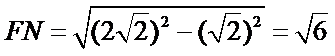
在Rt△FBN中,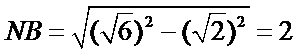

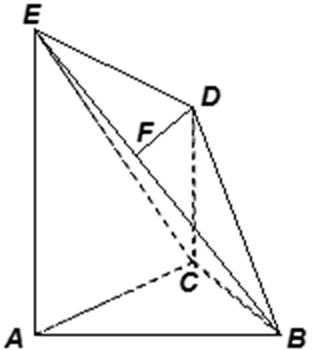
如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
19.证明:平面AEC⊥平面BED;
20.若∠ABC=120°,AE⊥EC,三棱锥—ACD的体积为
正确答案
正确答案
在如图所示的几何体中,平面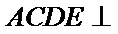
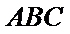
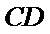
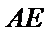
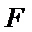
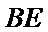
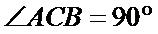
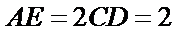
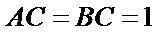
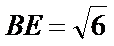
18.求证: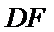
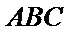
19.求证:
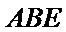
20.求三棱锥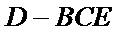
正确答案
证明:设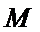
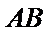

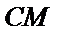
在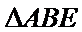
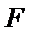
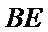
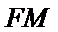
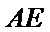
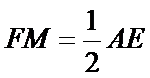
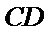
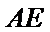
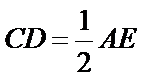
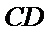
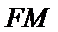
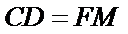
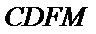
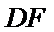
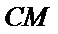
因为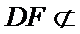
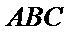
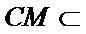
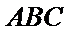
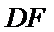
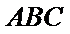

解析
证明:设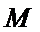
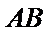

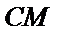
在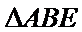
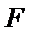
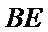
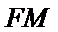
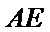
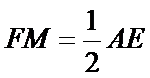
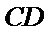
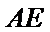
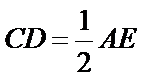
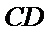
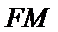
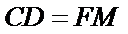
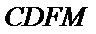
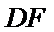
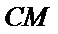
因为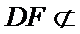
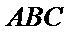
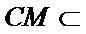
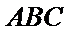
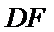
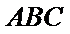

考查方向
直线和平面平行的判定
解题思路
取AB的中点,连接FM和CM,利用三角形中位线和平行线的性质,推导出线面平行成立的条件。
易错点
证明出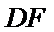
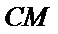
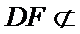
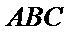
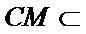
教师点评
本题考察学生做辅助线的能力,考查学生对三角形中位线,平行四边形的性质,以及直线与平面平行的判定定理的掌握程度。
正确答案
解:在直角三角形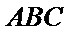
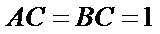
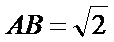
因为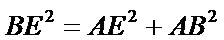
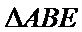
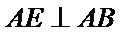
已知平面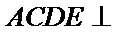
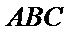
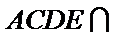
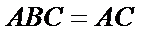
又因为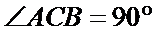

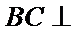
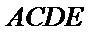
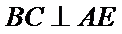
又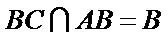
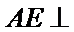
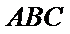
因为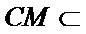
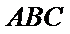
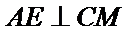
在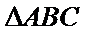
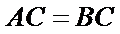
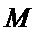
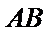
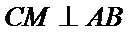
又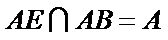
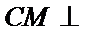
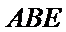
由(Ⅰ)知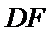
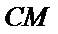
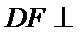

解析
解析:在直角三角形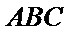
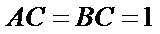
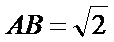
因为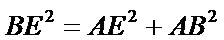
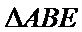
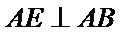
已知平面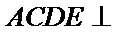
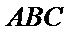
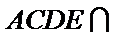
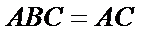
又因为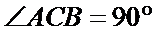

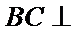
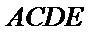
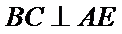
又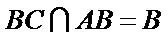
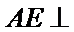
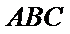
因为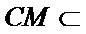
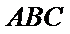
在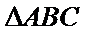
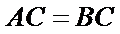
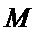
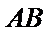
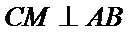
又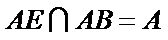
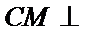
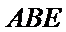
由(Ⅰ)知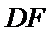
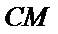
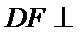

考查方向
直线与平面垂直的判定与性质。
解题思路
分别在三角形ABC和三角形ABE中应用勾股定理证明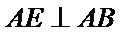
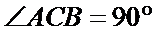
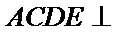
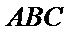
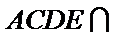
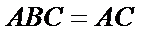
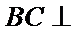
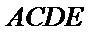
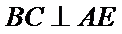
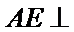
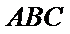
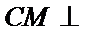
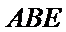
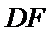
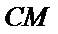
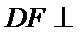
易错点
由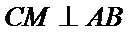
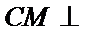
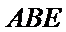
教师点评
本题难度中等,过程复杂,既考查了平面几何知识在立体几何中的灵活应用,又考察了直线和平面平行的判定和性质定理的应用。
正确答案
解:由(Ⅱ)知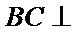
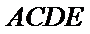
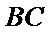
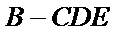
所以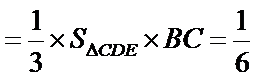
解析
解析:由(Ⅱ)知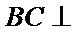
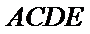
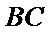
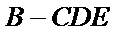
所以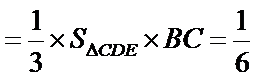
考查方向
棱锥的体积公式
解题思路
三棱锥可以把任何一个面作为底,顶点到底面的距离作为高。这里把三角形CDE做底,BC做高,容易计算体积。
易错点
把BCE作为三棱锥的地面,很难求出高。
教师点评
本题考察学生对三棱锥体积公式的灵活运用。
9.已知A,B是球O的球面上两点,∠AOB=90,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析