- 棱柱、棱锥、棱台的体积
- 共114题
19.在三棱锥




求证

正确答案
证明略;

解析
∵

∴


又∵
∴
故

在

∴
又在

∴
又∵

∴

考查方向
本题主要考查立体几何中两直线相互垂直的判定以及简单多面体的体积公式,考查逻辑推理能力以及计算能力,是容易题.
解题思路

易错点
线线垂直与线面垂直的相互转化,条件缺一不可.题中的证明,在证明线面垂直时,必须是平面外的直线分别垂直于平面上的两条相交直线,才能得到线面垂直.
知识点
4.若正三棱柱的所有棱长均为


正确答案
解析
知识点
5.某三棱锥的三视图如图所示,则该三棱锥四个面的面积中最大的是
正确答案
解析
根据三视图将几何体放到长方体中得到原来几何体为三棱锥








考查方向
解题思路
1、将几何体放到长方体中考虑;
2、得到原来的几何体后计算各个面的面积后选出面积的最大值。
易错点
无法由三视图还原到原来的几何体;
知识点
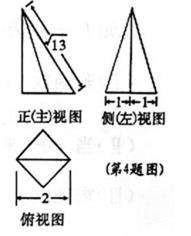
3.一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是( )
正确答案
解析
由图可知,
该四棱锥底面边长为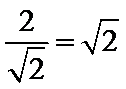
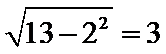
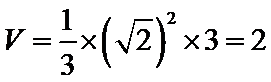
应选B.
考查方向
本题主要考查三视图和锥体的体积公式等知识,考查绘图,识图能力及空间想象能力。难度不大。
解题思路
1.画出立体图形,算出锥体的高;
2.利用体积公式计算,得出结果,应选B。
易错点
1.在求锥体的高时,不能正确找到里面的直角三角形求解;
2.用锥体的体积公式时,易遗漏前面有个1/3。
知识点
9.如图,四棱锥



正确答案
解析
考查方向
易错点
本题容易在没有发现B,D点的位置关系,导致无法解答
知识点
扫码查看完整答案与解析