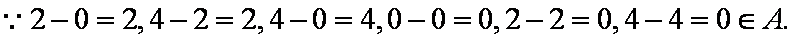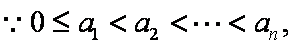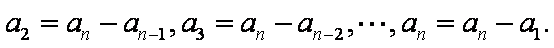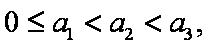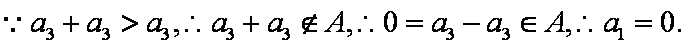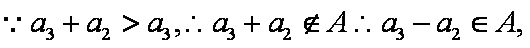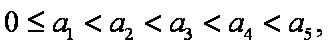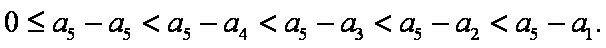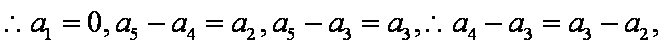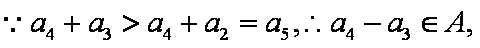- 两角和与差的余弦函数
- 共34题
已知集合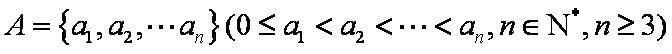
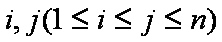
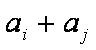
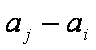
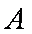
(1)分别判断集合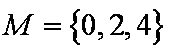
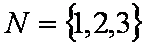
(2)①求证: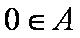
②求证: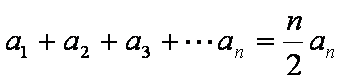
(3)研究当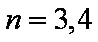
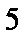
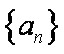
正确答案
见解析
解析
(1)对于集合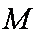
∴集合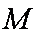
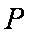
对于集合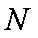
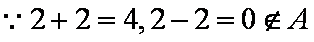
∴集合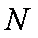
(2)①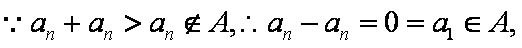
②
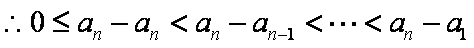
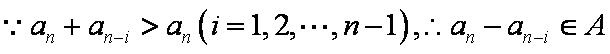
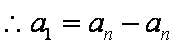

(3)①当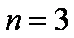
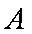
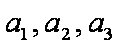
证明:当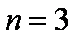
∴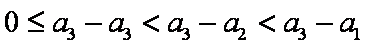
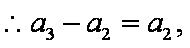
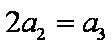
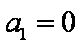
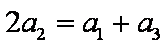
故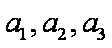
②当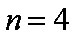
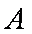
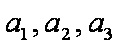
如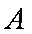
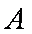
③当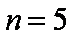
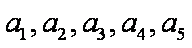
证明:当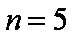
又
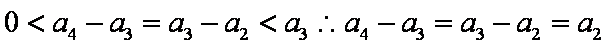
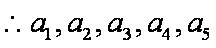
知识点
如图所示,扇形





过点



(1)若


(2)设


正确答案
(1)
解析
解析:
(1)在△

由
得

(2)∵


在△

∴

解法一:记△


∴


解法二:
即

当且仅当
所以




知识点
已知



正确答案
解析
∵


∴

∴

知识点
已知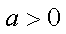
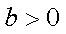
正确答案
见解析。
解析
先证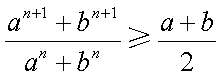
只要证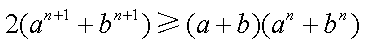
即要证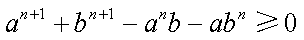
即要证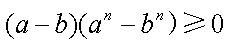
若
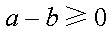
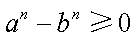
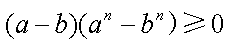
若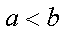
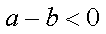
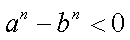
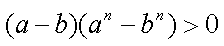
综上,得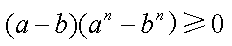
从而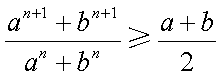
因为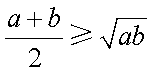
所以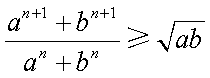
知识点
设

正确答案
解析
解析:由cos(A-C)+cosB=
cos(A-C)-cos(A+C)=
cosAcosC+sinAsinC-cosAcosC+sinAsinC=
sinAsinC=
又由b2=ac及止弦定理得sin2B=sinAsinC
故sin2B=
∴sinB=

于是B=

又由b2=ac知b≤a或b≤c ∴B=
知识点
扫码查看完整答案与解析