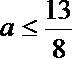- 指数与指数函数
- 共1021题
22.已知函数

(1)曲线




(2)




(3)




正确答案
解:(1)

∵曲线


∴ 

(2)设

又在点
∴
设

∴



从而,结合(Ⅰ)可知,满足题设的点
(3)当



曲线



由

∵ 曲线



即

若




从而,方程

令

∴ 当






∴





解析
解析已在路上飞奔,马上就到!
知识点
14.若方程
正确答案
解析
令函数




知识点
20. 已知椭圆




(Ⅰ)求椭圆
(Ⅱ)过原点的直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数



(1)求函数
(2)在△ABC中,角A、B、C所对的边分别为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.若函数




(1)判断下列函数,是否为“

(2)已知函数


正确答案
(1)解:①若

则存在实数对
即

而
因此

②对一切
使得
即存在常数对

故

(2)解:函数

设有序实数对
则
当

因此
当
则有
即
所以
当
满足

解析
解析已在路上飞奔,马上就到!
知识点
11.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知

(1)若


(2)若虚数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 若函数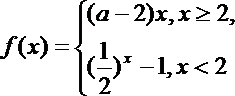

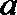
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.下列函数中,在其定义域内既是奇函数又是减函数的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析