- 平面与平面垂直的判定与性质
- 共129题
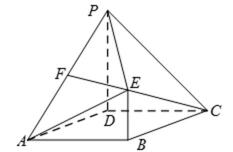
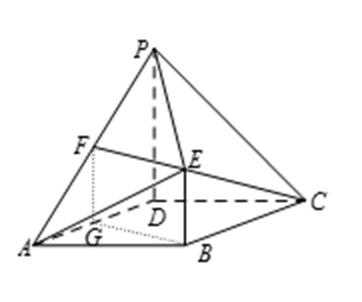
19.如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,E为AD上一点,F为PC上一点,四边形BCDE为矩形,∠PAD=60°,PB=2√3,PA=ED=2AE=2.(1)若




正确答案
见解析
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难.
(1)连接



因为



所以
因为

因为

所以
(2)因为
所以
所以
又平面





(3)由(2)知,
∴ ∠PBE为直线PB与平面ABCD所成的角,
在RtΔPEB中,


直线PB与平面ABCD所成的角为60°.
考查方向
解题思路
本题考查立体几何中的线面位置关系,解题步骤如下:1、利用线面平行的性质定理。2、利用线面垂直的定义及判定定理转化。
易错点
1、第一问中的线线平行的判定。2、第二问中求证线面垂直时要与平面内的两条相交直线垂直。
知识点
15.半径为1的球面上有四个点





正确答案
解析
由题意可知图形如图所示,
AB过点



考查方向
解题思路
根据图中的有关关系,确定图形的特征,将三棱锥


易错点
本题容易因对球面上的问题想象不到位,不能很好地寻求分割图形的策略而导致错误的出现。
知识点
18. 如图,四边形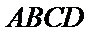
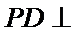
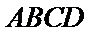
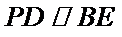
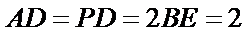
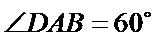
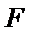
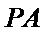
(Ⅰ)求证: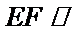
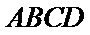
(Ⅱ)求证:平面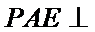
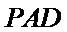
(Ⅲ)求三棱锥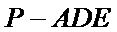
正确答案
(Ⅰ)略;
(Ⅱ)略;
(Ⅲ)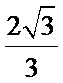
解析
(Ⅰ)取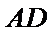
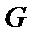
因为点
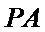
所以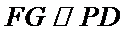
又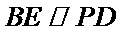
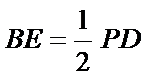
所以
所以四边形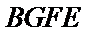
所以
又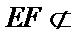
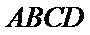
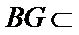
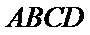
所以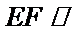
(Ⅱ)连接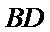
因为四边形
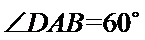

因为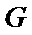
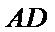
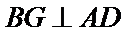
又因为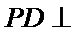
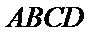
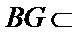
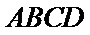
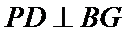
又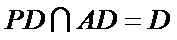
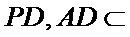
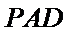
所以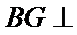
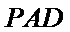
又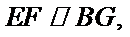
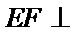
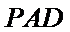
又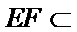
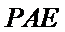
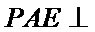
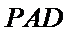
法二:因为四边形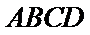
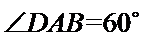
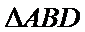
因为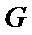
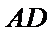
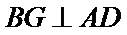
又因为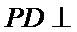
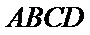
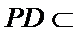
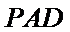
所以平面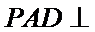
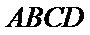
又平面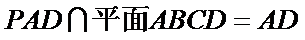
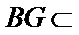
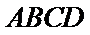
所以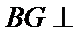
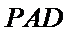
又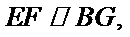
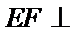
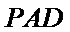
又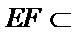
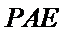
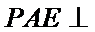

(Ⅲ)因为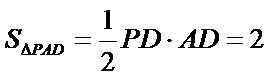
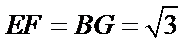
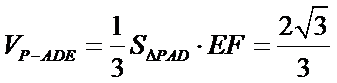
考查方向
本题考查了线面平行,面面垂直的证明,体积的求法,在近几年的各省高考题出现的频率非常高.
解题思路
(Ⅰ)借助于平行四边形,得到线线平行,进而得到线面平行;
(Ⅱ)利用面面垂直的判定定理;
易错点
定理记忆不清致误.
知识点
18.如图,在四棱锥


(I)求证:平面
(II)求三棱锥
正确答案
(1)见解析;
(2)
解析
本题属于立体几何应用中的基本问题,题目的难度不大,用到一些平面几何的知识。
(1)化为求线面垂直
(2)转变思想,换个角度看问题。
(I)连接BQ,因为ABCD是直角梯形,AD∥BC,AD=2BC,Q为AD的中点,
所以BCDQ为平行四边形,又因为CD=

因为ΔPAD是边长为2的正三角形,Q是AD的中点,
所以PQ⊥AD,PQ=
在ΔPQB中,QB=


因为AD∩BQ=Q,AD、BQ
所以PQ⊥平面ABCD.
因为PQ
(II)由(I)知:PQ⊥平面ABCD,PQ=
因为底面ABCD为直角梯形,AD∥BC,∠ADC=
所以ΔBCD是直角三角形,其中∠BCD=
因为BC=1,CD=

考查方向
本题考查了空间面面垂直、求椎体体积等知识,全面考查了学生阅读能力、空间想象能力与分析问题解决问题的能力,属于中档题,立体几何也是高考的必考内容,常与平几知识相结合,也有的会需要建立空间坐标系,结合空间向量的知识解决。
易错点
第二问求三棱锥的体积,如果不知道转化,则无法求出.
知识点
18. 如图所示,该几何体是由一个直三棱柱



(Ⅰ)证明:平面

(Ⅱ)求正四棱锥


正确答案
略
解析
(Ⅰ)证明:直三棱柱









(Ⅱ)




考查方向
本题考查了立体几何中的面面垂直的证明和正四棱锥的体积问题,
解题思路
本题第一问证明面面垂直,只要证明线面垂直即可;第二问把两个几何体的体积求出来,由两个几何体的体积关系直接求出高就行了。
易错点
1、解题 的规范化问题,2、第二问中不能正确的求出所需几何体的体积。
知识点
扫码查看完整答案与解析