- 平面与平面垂直的判定与性质
- 共129题
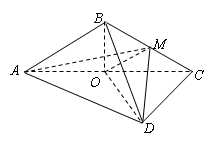
如图,四棱锥




(1)证明:平面

(2)求点
正确答案
见解析
解析
(1)如图取中点






且








(2) 由(1)可知







由题意可知四边形


设点








知识点
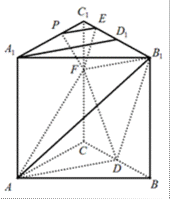
已知ABC是边长为3的等边三角形,点D、E分别是边AB、AC上的点,且满足==.将ADE沿DE折起到1ADE的位置,并使得平面A1DE⊥平面BCED.
(1)求证:A1D⊥EC;
(2)求三棱锥E-A1CD的高。
正确答案
见解析
解析
解析:(1)因为等边△

所以



由余弦定理得
因为
所以
折叠

因为平面







故A1D⊥EC.…………6分
(2)法一:由(2)的证明,可知


以
















所以


所以
因为







所以
①若


②若
令
因为函数

即
所以
故所求的最大值为
法二:如图,作



由(1)有



所以


所以






所以A1H=
所以在


①若x=0,则tan


②若

令
因为函数

所以tan

知识点
如图,菱形
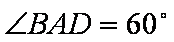
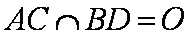
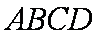
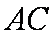
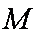
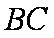
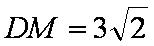
(1)求证: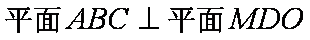
(2)求三棱锥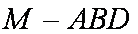
正确答案
见解析
解析
(1) 证明:由题意,
因为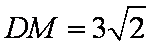
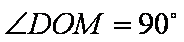
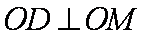
又因为菱形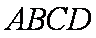
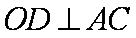
因为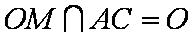
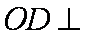
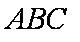
因为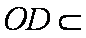
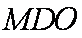
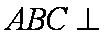
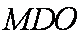
(2)解:三棱锥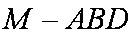
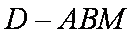
由(1)知,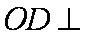
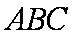
所以
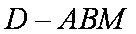
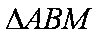
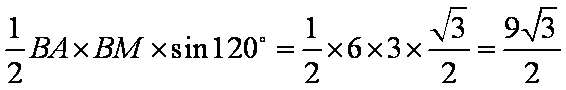
所求体积等于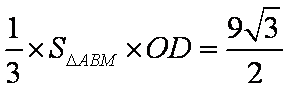
知识点
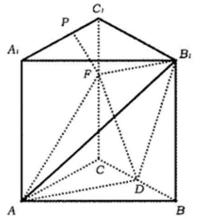
在直三棱柱ABC—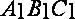
(1)求证:B1F⊥平面ADF;
(2)若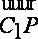
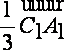
正确答案
见解析。
解析
(1)证明:
∵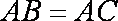
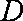
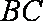
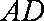
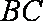
在直三棱柱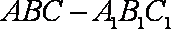
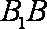
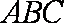
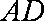
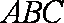
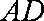
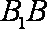
∵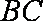
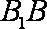
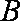
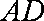
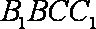
∵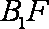
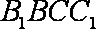
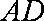
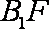
在矩形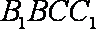
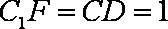
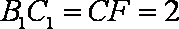
∴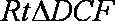
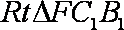
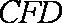
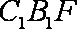
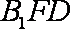
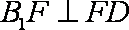
∵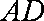
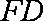
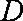
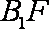
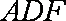
(2)取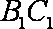
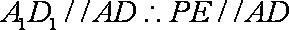
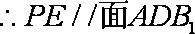
知识点
如图,菱形







(1)求证:
(2)求三棱锥
正确答案
见解析
解析
解析:(1) 证明:由题意,
因为


又因为菱形

因为


因为



(2)解:三棱锥

由(1)知,

所以



所求体积等于
知识点
扫码查看完整答案与解析