- 平面与平面垂直的判定与性质
- 共129题
1
题型:简答题
|
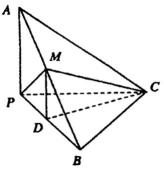
19.如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
(Ⅰ)求证:DM∥平面APC;
(Ⅱ)求证:平面ABC⊥平面APC;
(Ⅲ)若BC=4,AB=20,求三棱锥D-BCM的体积.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
棱柱、棱锥、棱台的体积直线与平面平行的判定与性质平面与平面垂直的判定与性质
1
题型:简答题
|
18. 如图,在三棱锥P-ABC中,PA
(I)证明:平面PBE
(II)在BC上找一点F,使AD∥平面PEF,并说明理由;
(III)在(II)的条件下,若PA=AB=2,求三棱锥B-PEF的体积.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
棱柱、棱锥、棱台的体积直线与平面平行的判定与性质直线与平面垂直的判定与性质平面与平面垂直的判定与性质
1
题型:
单选题
|
4.设a,b是两条直线,α,β是两个平面,则
正确答案
B
解析
解析已在路上飞奔,马上就到!
知识点
充分条件直线与平面平行的判定与性质直线与直线垂直的判定与性质直线与平面垂直的判定与性质平面与平面垂直的判定与性质
1
题型:简答题
|
19. 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是平行四边形,且AA1⊥底面ABCD,AB=2,AA1=BC=4,∠ABC=60°,点E为BC中点,点F为B1C1中点.
(Ⅰ)求证:平面A1ED⊥平面A1AEF;
(Ⅱ)求三棱锥E-A1FD的体积.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
棱柱、棱锥、棱台的体积直线与平面垂直的判定与性质平面与平面垂直的判定与性质
1
题型:简答题
|
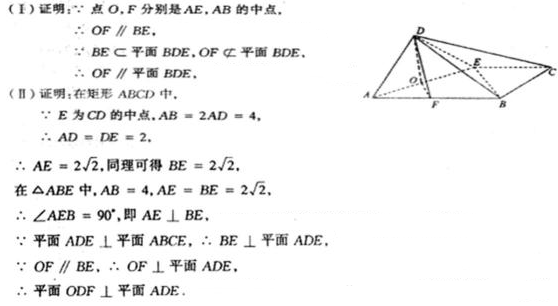
20. 已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△ADE折起,使平面ADE上平面ABCE,点O、F分别是AE、AB的中点。
(Ⅰ)求证:OF∥平面BDE;
(Ⅱ)平面ODF⊥平面ADE.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
直线与平面平行的判定与性质平面与平面垂直的判定与性质
下一知识点 : 直线、平面垂直的综合应用
扫码查看完整答案与解析