- 函数解析式的求解及常用方法
- 共158题
15.已知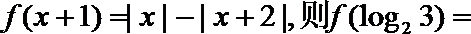
正确答案

解析
解析已在路上飞奔,马上就到!
知识点
20. 某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率p与日产量x(单位:件,x∈N*)间的关系为
(I)将日利润y(元)表示成日产量x(件)的函数;
(II)求该厂的日产量为多少件时,日利润最大?并求出日利润的最大值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.现有一张长为80cm,宽为60cm的长方形铁皮ABCD,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为100%,不考虑焊接处损失。如图,若长方形ABCD的一个角剪下一块正方形铁皮,作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,设长方体的底面边长为x (cm),高为y (cm),体积为V (cm3)
(1)求出x 与 y 的关系式;
(2) 求该铁皮盒体积V的最大值。
正确答案
解:(1)由题意得
即

(2)铁皮盒体积



因为





所以


答:该铁皮盒体积

解析
解析已在路上飞奔,马上就到!
知识点
19.甲乙两个学校高三年级分别有1100人,1000人,为了了解两个学校全体高三年级学生在该地区二模考试的数学成绩情况,采用分层抽样方法从两个学校一共抽取了105名学生的数学成绩,并作出了频数分布统计表如下:
甲校:
乙校:
(Ⅰ)计算x,y的值。
(Ⅱ)若规定考试成绩在[120,150]内为优秀,请分别估计两个学校数学成绩的优秀率;
(Ⅲ)由以上统计数据填写下面2×2列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异。
附:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数

(Ⅰ)如果函数

(Ⅱ)当


正确答案
解
(Ⅰ)∵

函数
∴

∴

.∵

∴
∴所求的

(Ⅱ)当


理由:当

它的定义域为


当


设
则
∴当


当


解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析









