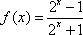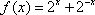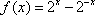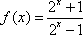函数解析式的求解及常用方法
共158题

· 函数解析式的求解及常用方法

函数解析式的求解及常用方法
共158题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

设满足约束条件则目标函数的最大值是；使取得最大值时的点的坐标是（） .

正确答案

3 ;

解析

略

知识点

函数解析式的求解及常用方法

题型：单选题

单选题 · 5 分

定义下列四个函数中,当自变量变为原来的2倍，函数值变为原来的4倍的函数是

A函数，其中自变量为球半径，函数值为此球的体积

B函数，其中自变量为圆锥底面半径，函数值为此圆锥的体积

C函数，函数值为数据都扩大倍后新数据的标准差

D函数，其中自变量为球的表面积，函数值为此球的体积。

正确答案

解析

略。

知识点

函数解析式的求解及常用方法

题型：单选题

单选题 · 5 分

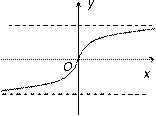
如右图所示的函数图像,则它所对应的函数解析式为

正确答案

解析

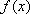
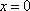
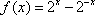
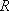
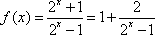
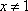
通过图像可以分析出在处有意义且为奇函数,增函数,函数值有上下界。为偶函数, 值域为,为减函数且定义域中，故只有A。

知识点

函数解析式的求解及常用方法

题型：简答题

简答题 · 12 分

函数的部分图象如下图所示，该图象与轴交于点，与轴交于点，为最高点，且三角形的面积为。

（1）求函数的解析式；

（2）若，求的值。

正确答案

见解析。

解析

（1）∵，

∴周期。

由，得，

∵，∴，

∴。

（2）由，得，

∵，

∴，

∴

。

知识点

函数解析式的求解及常用方法

题型：简答题

简答题 · 14 分

已知函数是定义在实数集R上的奇函数，当x>0时，，其中

常数。

（1）求函数的解析式；

（2）若函数在区间上是单调减函数，求a的取值范围；

（3）函数的导函数，问是否存在实数，使得对任意实数a，都有成立？若存在，请求出的值；若不存在，请说明理由。

正确答案

见解析。

解析

⑴，时，，所以

⑵函数是奇函数，则在区间上单调减少，当且仅当在区间上单调减少，当时，，，由得，在区间的取值范围为，所以的取值范围为

⑶存在。…，解

，得，因为，所以为所求。

知识点

函数解析式的求解及常用方法

继续学习学习下一知识点

下一知识点 : 区间与无穷的概念

百度题库 > 高考 > 文科数学 > 函数解析式的求解及常用方法

扫码查看完整答案与解析