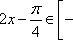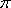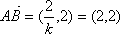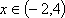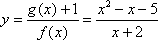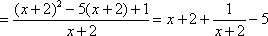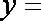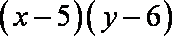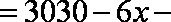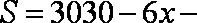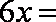- 函数解析式的求解及常用方法
- 共158题
某市地铁连同站台等附属设施全部建成后,平均每1公里需投资人民币1亿元.全部投资都从银行贷款.从投入营运那一年开始,地铁公司每年需归还银行相同数额的贷款本金0.05亿元.这笔贷款本金先用地铁营运收入支付,不足部分由市政府从公用经费中补足. 地铁投入营运后,平均每公里年营运收入(扣除日常管理费等支出后)第一年为0.0124亿元,以后每年增长20%,到第20年后不再增长。
(1)地铁营运几年,当年营运收入开始超过当年归还银行贷款本金?
(2)截至当年营运收入超过当年归还银行贷款本金的那一年,市政府已累计为1公里地铁支付多少元费用?(精确到元,1亿=
正确答案
见解析
解析
(1)地铁营运第


根据题意有:
解得
(或者

答:地铁营运9年,当年营运收入开始超过当年归还银行贷款本金. ……6分
(2)市政府各年为1公里地铁支付费用
第1年:
第2年:
。。。。。。
第



将

答:截至当年营运收入超过当年归还银行贷款本金的那一年,市政府累计为1公里地铁共支付19541135元费用. ………………………………14分
知识点
一自来水厂用蓄水池通过管道向所管辖区域供水,某日凌晨,已知蓄水池有水9千吨,水厂计划在当日每小时向蓄水池注入水2千吨,且每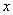
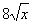
(1)多少小时后,蓄水池存水量最少?
(2)当蓄水池存水量少于3千吨时,供水就会出现紧张现象,那么当日出现这种情况的时间有多长?
正确答案
见解析
解析
(1)设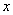
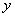
依题意,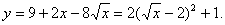
当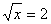
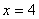
(2)依题意,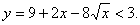
解得: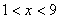
所以,当天有8小时会出现供水紧张的情况。 ………………………………1分
知识点
已知向量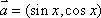
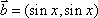
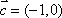
(1)若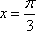
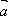
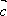
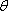
(2)若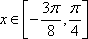
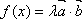

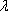
正确答案
见解析
解析
(1)当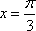
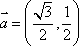
所以 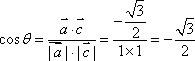
因而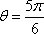
(2)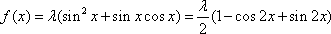

因为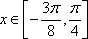
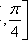
当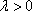
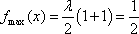
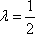
当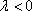
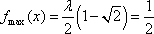
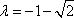
所以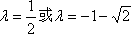
知识点
已知二次函数




(1)求函数
(2)求函数
正确答案
见解析。
解析
(1)








故函数
(2) 


··
当

又
故函数
知识点
已知函数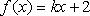
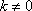

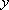
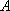
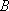
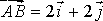
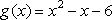

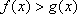
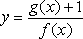
正确答案
-3
解析
由题意知: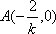
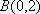
可解得: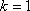
因为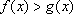
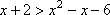
因为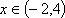
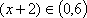
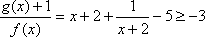
当且仅当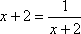
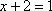
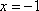
所以,当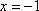
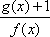
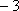
知识点
某地政府为改善居民的住房条件,集中建设一批经适楼房。用了1400万元购买了一块空地,规划建设8幢楼,要求每幢楼的面积和层数等都一致,已知该经适房每幢楼每层建筑面积均为250平方米,第一层建筑费用是每平方米3000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加80元。
(1)若该经适楼房每幢楼共


(2)要使该批经适房的每平方米的平均开发费用最低,每幢楼应建多少层?
正确答案
见解析
解析
(1)由已知,每幢经适楼房最下面一层的总建筑费用为:


从第二层开始,每幢每层的建筑总费用比其下面一层多:


每幢经适楼房从下到上各层的总建筑费用构成以75为首项,2 为公差的等差数列,2分
所以函数表达式为:

(2)由(1)知经适楼房每平方米平均开发费用为:


当且仅当

但由于




答:该经适楼建为13层时,每平方米平均开发费用最低, (14分)
知识点
定义:对函数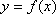
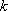
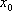
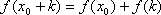
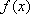
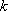
(1)若函数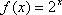
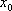
(2)判断函数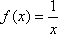
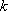
(3)若函数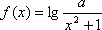

正确答案
见解析
解析
(1)由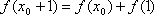
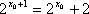
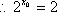
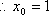
(2)若存在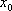

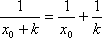
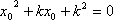
……………………………. 7分
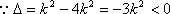

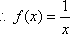
“k性质函数”。 ……………………………. 10分
(3)由条件
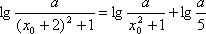
即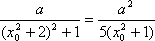
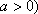
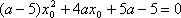
当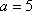
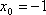
当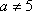

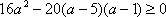
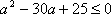
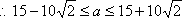
综上,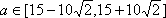
知识点
已知




(1) 求
(2) 设




正确答案
见解析
解析
(1)如图,在


可得
又 


则函数

其中定义域为
说明:亦可用积化和差方法化简:

(2)
由


1




2




因而存在实数


知识点
某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场,其总面积为3000平方米,其中场地四周(阴影部分)为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为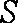
(1)分别写出
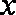
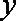
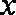
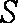
(2)怎样设计能使S
正确答案
见解析。
解析
(1)由已知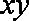
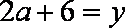
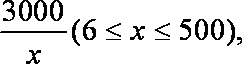

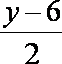
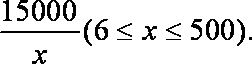
(2)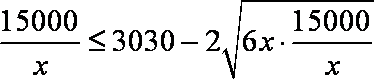
当且仅当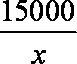


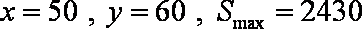
即设计x=50米,y=60米时,运动场地面积最大,最大值为2430平方米。 ……………(12分)
知识点
我国发射的天宫一号飞行器需要建造隔热层.已知天宫一号建造的隔热层必须使用20年,每厘米厚的隔热层建造成本是6万元,天宫一号每年的能源消耗费用C(万元)与隔热层厚度


(1)求C(

(2)当陋热层修建多少厘米厚时,总费用
正确答案
见解析。
解析
(1)当



(2)
当且仅当
即隔热层修建5厘米厚时,总费用达到最小值,最小值为70万元.……………12分
知识点
扫码查看完整答案与解析