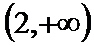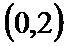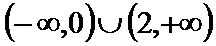函数性质的综合应用
共25题

· 函数性质的综合应用

函数性质的综合应用
共25题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

12．已知函数定义在R上的奇函数，当时，，给出下列命题：

①当时，

②函数有2个零点

③的解集为

④，都有

其中正确命题个数是（）

正确答案

解析

因为f(x)为R上的奇函数，设x>0，-x<0,则，所以1错误，因为，所以f(x)有三个零点，所以2错误，，因为当，

当所以所以解集为，所以3正确。

同理判断4正确，所以选B

考查方向

函数的性质及应用；导数的综合应用；函数奇偶性的性质

解题思路

根据函数的相关性质，结合子题目，依次判断

易错点

求导错误；

知识点

函数性质的综合应用函数零点的判断和求解

题型：单选题

单选题 · 5 分

11．已知定义在R上的奇函数满足，若，，则实数的取值范围为（）

正确答案

解析

，，所以可求出的周期为8,所以，所以，所以可得a的取值范围为

考查方向

奇函数的性质，周期函数；解不等式

解题思路

先根据奇函数性质求出函数周期，进而求出f(-7)的值，然后判断实数a的取值范围

易错点

不能利用相关性质求出周期

知识点

函数单调性的性质函数奇偶性的性质函数性质的综合应用

题型：单选题

单选题 · 5 分

5.函数(－π≤x≤π且x≠0)的图象可能为（）

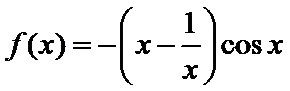
正确答案

解析

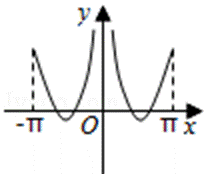
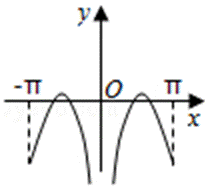
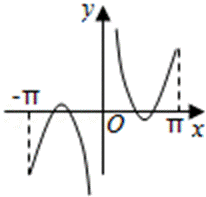
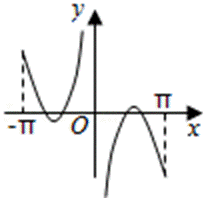
试题分析：根据函数的奇偶性判断出函数图象的对称性，利用0＜x＜1时函数值的正负进一步排除得出答案。

对于函数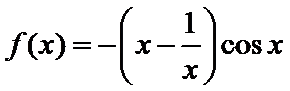（﹣π≤x≤π且x≠0），由于它的定义域关于原点对称，

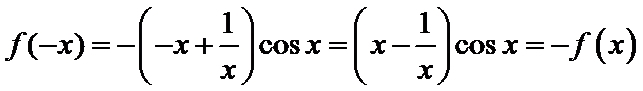
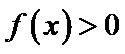
且满足，故函数f（x）为奇函数，故它的图象关于原点对称．且当0＜x＜1时，，故选C.

考查方向

本题主要考查函数的奇偶性的判断，奇函数的图象特征，函数的定义域和值域，属于中等题．

解题思路

由条件可得函数f（x）为奇函数，故它的图象关于原点对称；再根据但是当x趋向于0时，f（x）＞0，结合所给的选项，得出结论．

易错点

判断函数的奇偶性首先要看函数的定义域.

知识点

函数的图象函数性质的综合应用

题型：简答题

简答题 · 13 分

已知函数．

24.当时，求的极值；

25.当时，讨论的单调性；

26.若对于任意的都有，求实数的取值范围．

第(1)小题正确答案及相关解析

正确答案

（Ⅰ）当时，取得极小值为，无极大值．

解析

（Ⅰ）当时，，定义域为，

的导函数．

当时，，在上是减函数；

当时，，在上是增函数．

∴当时，取得极小值为，无极大值．

考查方向

本题主要考查利用导数研究函数极值、函数单调性、恒成立问题等知识，意在考查考生的分类讨论、转化的数学思想及综合应用知识的能力。

解题思路

直接求导，判断导数的正负后即可得到极值；

易错点

无

第(2)小题正确答案及相关解析

正确答案

（Ⅱ）当时，在上是减函数，在上是增函数；

当时，在上是减函数；

当时，在上是减函数，在上是增函数．

解析

（Ⅱ）当时，的定义域为，的导函数为．

由得，，．

（1）当时，在上是减函数，在上是增函数，在上是减函数；

（2）当时，在上是减函数；

（3）当时，在上是减函数，在上是增函数，

在上是减函数．

综上所述，

当时，在上是减函数，在上是增函数；

当时，在上是减函数；

当时，在上是减函数，在上是增函数．

考查方向

本题主要考查利用导数研究函数极值、函数单调性、恒成立问题等知识，意在考查考生的分类讨论、转化的数学思想及综合应用知识的能力。

解题思路

求导后分类讨论导数的正负后确定函数的单调区间；

易错点

在求函数的单调性时，不会确定分类的标准；

第(3)小题正确答案及相关解析

正确答案

（Ⅲ）．

解析

（Ⅲ）由（Ⅱ）知，当时，在上是减函数．

∴．

∵对于任意的都有，

∴对任意恒成立，

∴对任意恒成立．

当时，，∴．

∴实数的取值范围为．

考查方向

本题主要考查利用导数研究函数极值、函数单调性、恒成立问题等知识，意在考查考生的分类讨论、转化的数学思想及综合应用知识的能力。

解题思路

先根据第（2）问放缩后构造不等式后分类参数即可求解。

易错点

不会放缩

题型：单选题

单选题 · 5 分

10. 若为偶函数，则的解集为（）

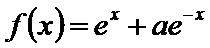
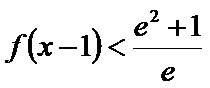
正确答案

解析

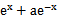
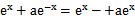
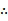
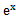
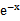
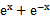
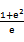
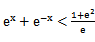
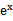
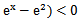
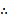
若f(x)=为偶函数，则f(x)=f(-x),即,(1-a)(-)=0,a=1, f(x)=, f(x-1)< ,，(-1)(，0

考查方向

函数的奇偶性，解不等式

解题思路

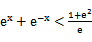
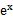
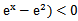
先由偶函数性质，求出a=1，将不等式进行化简整理，(-1)(，解出取值范围，进而求出x的取值范围

易错点

不等式的化简整理

知识点

函数奇偶性的性质函数性质的综合应用不等式与函数的综合问题

继续学习学习下一知识点

下一知识点 : 求函数的值

百度题库 > 高考 > 文科数学 > 函数性质的综合应用

扫码查看完整答案与解析