- 函数性质的综合应用
- 共25题
7.下列判断错误的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.给出下列几个命题:
①若函数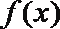


②若函数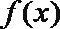

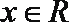

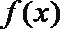
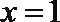
③已知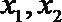
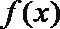
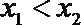
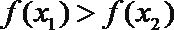
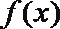
④设函数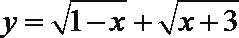
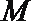
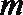
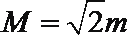
⑤若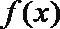
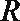
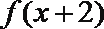
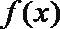
其中正确的命题序号是___________.(写出所有正确命题的序号)
正确答案
①④⑤
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数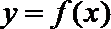
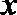
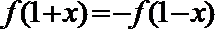
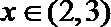
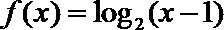
① 函数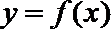
② 函数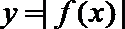
③ 当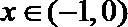
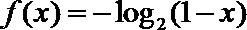
④ 函数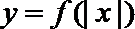
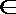
其中所有正确结论的序号为
正确答案
①②③
解析
解析已在路上飞奔,马上就到!
知识点
23.已知函数



(1)求
(2)问:是否存在边长为







(3)若函数




正确答案
(1)把

可得:
化简此方程组可得:
即
可得

代入原方程组可得:
(2)由

此三角形的高即点






即





直线
即
(3)由题意知:












又


解析
解析已在路上飞奔,马上就到!
知识点
18.若



①

②

③


④函数


则以上各命题中正确的个数是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析























