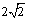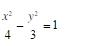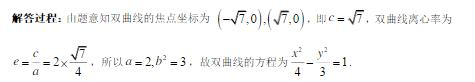双曲线及其性质
共445题

双曲线及其性质
共445题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

10.

正确答案

解析

设公共切点的横坐标为

依题意有

两式相除可得，故

考查方向

导数与切线方程

解题思路

根据导数的集合性质，建立等量关系，然后利用两个等式关系，化简整理求得答案

易错点

不会利用导数求曲线的切线方程

知识点

双曲线的定义及标准方程

题型：单选题

单选题 · 5 分

8.已知抛物线与双曲线的一个交点为，为抛物线的焦点，若，则该双曲线的渐近线方程为（　）

正确答案

解析

根据题意可知，抛物线焦点F(2,0)，因为MF=5,所以，所以代入得到，所以令得到双曲线的渐近线为即

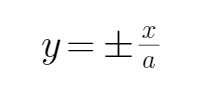
考查方向

双曲线的性质抛物线的性质

解题思路

设出相关点的坐标，找到等量关系建立方程，然后求出参数。进而得到渐近线方程

易错点

计算能力弱，相关公式记忆混淆

知识点

双曲线的定义及标准方程

题型：填空题

填空题 · 4 分

若实数满足，则的最小值为.

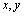
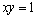
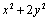
正确答案

解析

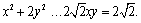
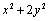
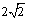
由基本不等式可得故的最小值为.

知识点

双曲线的几何性质

题型：单选题

单选题 · 5 分

已知双曲线：的离心率为2.若抛物线的焦点到双曲线的渐近线的距离为2，则抛物线的方程为

正确答案

解析

抛物线的焦点，双曲线的渐近线为，不妨取，即，焦点到渐近线的距离为，即，所以双曲线的离心率为，所以，所以，所以抛物线方程为，选D.

知识点

双曲线的几何性质抛物线的标准方程和几何性质

题型：填空题

填空题 · 4 分

已知双曲线的一条渐近线的方程为，则。

正确答案

解析

由得渐近线的方程为即，由一条渐近线的方程为得2。

知识点

双曲线的几何性质

题型：单选题

单选题 · 5 分

设a，b是关于t的方程t2cosθ+tsinθ=0的两个不等实根，则过A（a，a2），B（b，b2）两点的直线与双曲线﹣=1的公共点的个数为（　　）

正确答案

解析

∵a，b是关于t的方程t2cosθ+tsinθ=0的两个不等实根，

∴a+b=﹣，ab=0，

过A（a，a2），B（b，b2）两点的直线为y﹣a2=（x﹣a），即y=（b+a）x﹣ab，

即y=﹣x，

∵双曲线﹣=1的一条渐近线方程为y=﹣x，

∴过A（a，a2），B（b，b2）两点的直线与双曲线﹣=1的公共点的个数为0。

知识点

双曲线的几何性质直线与双曲线的位置关系

题型：填空题

填空题 · 4 分

已知双曲线和椭圆有相同的焦点，且双曲线的离心率是椭圆离心率的两倍，则双曲线的方程为 .

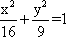
正确答案

解析

知识点

椭圆的几何性质双曲线的定义及标准方程双曲线的几何性质

题型：单选题

单选题 · 5 分

已知双曲线的左顶点与抛物线的焦点的距离为4，且双曲线的一条渐近线与抛物线的准线的准线的交点坐标为（-2，-1），则双曲线的焦距为（）

正确答案

解析

双曲线的渐近线为，由双曲线的一条渐近线与抛物线的准线的交点坐标为（－2，－1）得，即，

又∵，∴，将（－2，－1）代入得，

∴，即

知识点

双曲线的几何性质

题型：单选题

单选题 · 5 分

11.设,分别为双曲线的左,右焦点.若在双曲线右支上存在一点,满足,且到直线的距离等于双曲线的实轴长,则该双曲线的离心率为（）

正确答案

解析

可得|PF2|=|F1F2|=2c,故可得|PF1|=4b,则|PF1|-|PF2|=2a,再由b2=c2-a2及e=c/a可得。

考查方向

本题考查双曲线的标准方程和简单几何性质。

解题思路

根据焦点三角形的特征，列a,b,c的方程，转化为e的方程解即可。

易错点

无法得到方程；或解方程错误。

教师点评

本题考查了双曲线的定义，方程，几何性质知识，在近几年的各省高考题出现的频率较高，常与解三角形等知识点交汇命题。

知识点

双曲线的定义及标准方程双曲线的相关应用

题型：单选题

单选题 · 5 分

7. 焦点为，且与双曲线有相同的渐近线的双曲线方程是（）

正确答案

解析

由所求双曲线与双曲线有相同的渐近线，设所求双曲线的方程为双曲线，即，所以，所以。选B

考查方向

考查双曲线的渐近线概念，以及双曲线中，a，b,c的关系。

解题思路

由所求双曲线与已知双曲线共渐近线，设出双曲线方程，利用焦点在y轴上，得到关于的方程得解.

易错点

熟悉双曲线的渐近线与方差之间的关系。

知识点

双曲线的定义及标准方程双曲线的几何性质

继续学习学习下一知识点

下一知识点 : 抛物线及其性质

百度题库 > 高考 > 文科数学 > 双曲线及其性质

扫码查看完整答案与解析