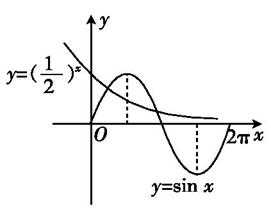
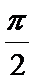- 正弦函数的图象
- 共40题
3.函数
正确答案
知识点
9.定义在区间[0,3π]上的函数y=sin2x的图象与y=cosx的图象的交点个数是 .
正确答案
7
知识点
15.已知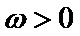
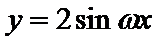
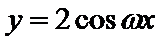
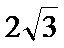
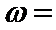
正确答案
解析
由题根据三角函数图像和性质可得交点坐标为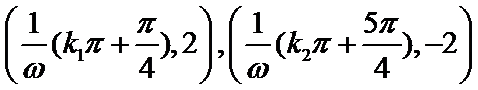
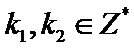
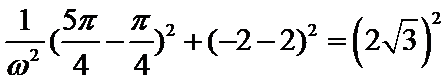
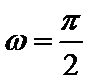
考查方向
解题思路
由题奋进三角函数的周期性求得两个函数的交点坐标,根据距离最短的两个交点一定在同一个周期,结合勾股定理不难得到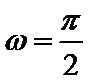
易错点
不能理解题中给出的条件导致没有办法入手解决。
知识点
8.将函数

正确答案
解析
将函数图像上各点的横坐标伸长到原来的3倍,可得到函数为:
再把函数图象向右平移


考查方向
解题思路
先得到变换后的函数,再根据函数图象对称性得到对称中心
易错点
变换规律掌握不好
知识点
9.已知函数


正确答案
解析
根据平移后与原函数重合可知平移的距离为周期可知

考查方向
解题思路
该题解题思路
1)根据平移后与原函数重合可知平移的距离为周期的整数倍
2)使用周期与
3)利用解析式求最值得到结果
易错点
主要易错于无法理解与原图重合对应的含义
知识点
6.已知函数



正确答案
解析
把图象上的点







B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
解题思路
代入法。把图象上的点代入,求出

易错点
易错选为C。
知识点
12.已知函数f(x)=|sin x|的图象与直线y=kx(k>0)有且仅有三个交点,交点的横坐标的最大值为α,令m=

正确答案
解析
作出函数f(x)=|sin x|的图象与直线y=kx(k>0)的图象,如图. 

当x∈
此时f'(x)=-cos x,则-cos α=-
所以m= 
知识点
7.方程(
正确答案
2
解析
如图,方程(
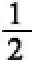
知识点
15.若不等式logax>sin2x(a>0,a≠1)对任意x∈(0,
正确答案
解析
记y1=logax,y2=sin2x,原不等式相当于y1>y2
作出两个函数的图象,如图所示
可知当y1=logax过点A(
所以当

知识点
7.将函数





正确答案
解析
考查方向
解题思路
易错点
知识点
扫码查看完整答案与解析