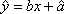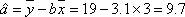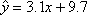- 独立性检验
- 共3题
13.给出下列命题: ①线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱; ②由变量x和y的数据得到其回归直线方程L:y =bx + a,则L一定经过点P(x,y);③从匀速传递的产品生产流水线上


正确答案
②④⑤.
解析
①线性相关系数|r|越大,两个变量的线性相关性越强,故①不正确;
②由变量x和y的数据得到其回归直线方程l:y=bx+a,则l一定经过点P故②正确;
③从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样不是分层抽样,故③不正确;
④可用残差平方和判断模型的拟合效果,残差平方和越小,模型的拟合效果越好,故④正确;
⑤在回归直线方程y=0.1x+10中,当解释变量x每增加一个单位时,预报变量平均增加0.1个单位,故⑤正确.
考查方向
本题线性相关、回归直线方程和拟合等相关概念。
解题思路
认真读题,挨个判断命题的真假
易错点
对上述概念理解的不透彻
知识点
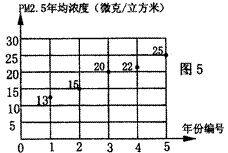
近年来,随着以煤炭为主的能源消耗大幅攀升、机动车保有量急剧增加,某市空气中的“pm2.5”(直径小于等于2.5微米的颗粒物)的含量呈逐年上升的趋势,图5是根据该市环保部门提供的2007年至2011年该市“pm2.5"年均浓度值画成的散点图,(为便于计算把2007年编号为1,2008年编号为2,……,2011年编号为5.)
(1)以“pm2.5”年均浓度值为因变量,年份的编号为自变量,利用散点图提供的数据,用最小二乘法求出该市“pm2.5”年均浓度值与年份编号之间的线性回归方程
(2)按世界卫生组织(WHO)过渡期一1的标准,空气中“pm2.5”的年均浓度限值为35微克/立方米,该市若不采取措施,试预测从2012年起,几年后该市空气中“pm2.5”的年均浓度值将超过世界卫生组织(WHO)过渡期一1设定的限值。
(温馨提示:答题前请仔细阅读卷首所给的计算公式及说明,)
正确答案
见解析。
解析
(1)由散点图可得,变量 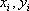
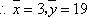
∴所求回归方程为
(2)由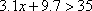
∴
故可预测从2012年起,3年后该市空气中“pm2.5”的年均浓度值将超过世界卫生组织( WHO)过渡期1设定的限值。
知识点
通过随机询问某校
(1)从这

(2) 从(1)中的
(3)根据以上列联表,问有多大把握认为“性别与在购买食物时看营养说明”有关?
正确答案
见解析。
解析
解:(1)根据分层抽样可得:样本中看营养说明的女生有

(2)记样本中看营养说明的





基本事件为:









其中事件
个的基本事件: 




所以所求的概率为
(3) 假设

根据题中的列联表得
由
有
知识点
扫码查看完整答案与解析