- 与圆有关的比例线段
- 共90题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
如图,弦AB与CD相交于O内一点E,过E作BC的平行线与AD的延长线交于点P,已知PD=2DA=2,则PE=__________.
正确答案
解析
∠C与∠A在同一个O中,所对的弧都是

知识点
如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则
正确答案
解析


知识点
如图,
(1)证明:
(2)若


正确答案
见解析。
解析
(1)由已知条件,可得
因为
故△ABE∽△ADC.
(2)因为△ABE∽△ADC,所以
又S=



则sin


知识点
如图,过点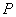

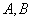
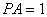
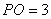
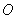
正确答案
解析
设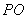
知识点
如图,圆






于点

正确答案
解析
连结



知识点
如图,











正确答案
2
解析










知识点
如图4,已知








正确答案
解析
略
知识点
如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线

正确答案
4
解析
连接AC,则AC⊥BC,由条件得AC=4
∠DCA=60°,所以DC=2
求得DE=2,可得AE=AD-DE =4
知识点
选考题:(从下列三道解答题中作选一题作答,若多做,则按首做题计入总分)
22.选修4-1:几何证明选讲
如图,四边形ABCD内接于





(1)证明:

(2)如果

23.选修4-4:坐标系与参数方程选讲
极坐标系与直角坐标系







(1)求证:|OB|+|OC|=
(2)当
24.选修4—5:不等式选讲
已知函数
(1)a =-3时,求不等式
(2)若关于x的不等式
22.选修4-1:几何证明选讲
如图,四边形ABCD内接于⊙






(1)证明:

(2)如果

23.选修4-4:坐标系与参数方程选讲









(1)求证:|OB|+|OC|=
(2)当

24.选修4—5:不等式选讲
已知函数
(1)a =-3时,求不等式 
(2)若关于x的不等式 
正确答案
正确答案
正确答案
扫码查看完整答案与解析