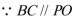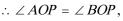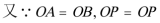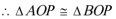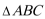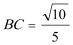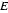- 与圆有关的比例线段
- 共90题
22. 【选修4-1:几何证明选讲】
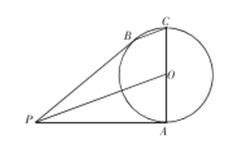
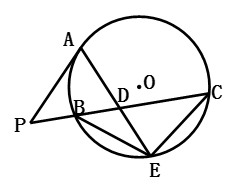
如图,已知线段AC为⊙O 的直径,P为⊙O的切线,切点为A,B为⊙O上一点,且BC∥PO.
( I )求证:PB为⊙O的切线;
(Ⅱ)若⊙O的半径为1,PA =3,求BC的长。
正确答案
(1)证明略;(2)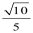
解析
试题分析:本题属于平面几何问题,题目难度较低,解题时要注意深入分析已知条件和特征结论,善于将各已知条件联系起来考虑,寻找合理的解题思路。
(1)连接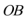
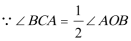
又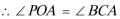
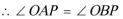
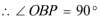
(2)连接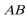
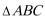
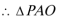
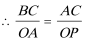
解得
考查方向
解题思路
本题考查三角形与圆的相关知识,解题步骤如下:
1、通过相应的条件和定理建立起有关角或边之间的关系式,如全等关系。
2、灵活三角形相似得到所需结论。
易错点
1、未想到连接OB、AB而无法下手;
2、第二问中由相似得到合适结论出错。
知识点
7. 如图,










正确答案
解析
由题可知,CD•DT=AD•DB,解得圆的半径CT=2r=11,由PT2=PB•PA,解得PB=14.
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
利用切割线定理求解即可.
易错点
本题易在利用切割线定理和割线定理时发生错误。
知识点
本题为选做题,请考生在第22、23、24三题中任选一题做答。如果多做。则按所做的第一题记分.作答时用2B铅笔在答题卡上把所选题目的题号涂黑.
22.选修4—l:几何证明选讲如图,∠BAC的平分线与BC和△ABC的外接圆分别相交于D和E,延长AC交过D、E、C三点的圆于点F.(Ⅰ)求证:EC=EF;(Ⅱ)若ED=2,EF=3,求AC·AF的值.
23.选修4—4:坐标系与参数方程 已知曲线C1的参数方程为


24.选修4—5:不等式选讲 已知函数f(x)=|x-2|-|x+1|.(Ⅰ)解不等式f(x)>1;(Ⅱ)当x>0时,函数g(x)=
正确答案
22.略.
23.(1)

24.(1)

解析
22. ⑴证明:因为





⑵解:因为






23. ⑴解:




⑵解:








24.⑴解:当








⑵解:因为






考查方向
22.本题考查了平面几何的知识,主要涉及直线与圆的位置关系,三角形相似的考查.
23.本题考查了参数方程的知识,主要涉及直线与圆的位置关系.
24.本题考查了不等式的知识,主要涉及绝对值不等式的解法
解题思路
22解题步骤如下:1、利用圆的相关定理证明。2、利用切割线定理和相交弦定理证明。
23解题步骤如下:1、利用公式消参。2、可以利用普通方程求解。
24.解题步骤如下:1、利用公式解绝对值不等式。2、可以利用图像求解。
易错点
22.相关的定理容易混用。
23.消参的过程容易出错。
24.去绝对值时容易出错。
知识点
22.如图,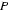
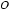
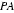
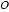
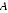
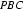
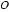
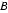
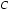
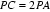
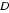
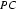
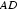
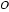
证明:(Ⅰ)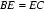
(Ⅱ)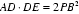
正确答案
略
解析
试题分析:本题属于平面几何中的基本问题,题目的难度是容易题。
(Ⅰ)证明:连接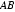
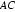

因为: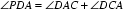
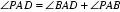
由弦切角等于同弦所对的圆周角: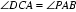
所以: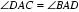

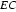
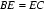
(Ⅱ)由切割线定理得: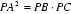
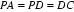
所以: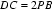
由相交弦定理得:
所以: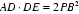
考查方向
本题考查了平面几何的知识,主要涉及直线与圆的位置关系,三角形相似的考查.
解题思路
本题考查平面几何的知识,解题步骤如下:
1、利用圆的相关定理证明。
2、原来切割线定理和相交弦定理证明。
易错点
相关的定理容易混用。
知识点
22.选修4-1几何证明选讲如图,
















23. 选修4-4极坐标与参数方程
已知曲线










24选修4-5不等式证明选讲已知函数






正确答案
22.(1)连接








(2)由




23. (1)曲线
(2)曲线





24. (1)要





解析
22. 连接














23. (1)曲线








24. 题意说明不等式






考查方向
22.圆周角定理,相似三角形的性质.23. 椭圆的参数方程,坐标变换,点到直线距离公式.24. 不等式有解问题,不等式的证明.
解题思路
22.利用圆周角定理计算,结合相似性质求解 23. 先求出直角坐标系下的椭圆方程,然后得到距离公式,进而判断最值24.利用集合的概念先解出不等式的解集,然后化简求解。
易错点
22.找相似条件 23. 参数方程的坐标转换,最值的判断 24. 基本不等式的应用,不等式的判断
知识点
扫码查看完整答案与解析