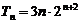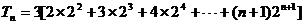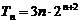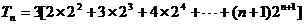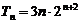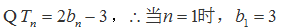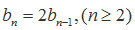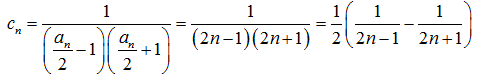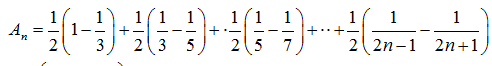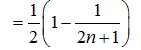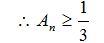- 由an与Sn的关系求通项an
- 共103题
19. 已知数列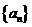
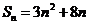
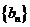
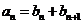
(I)求数列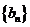
(II)令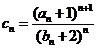
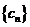
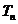
正确答案
(Ⅰ)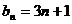
解析
试题分析:(Ⅰ)由题意得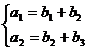
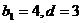
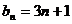
(Ⅱ)由(Ⅰ)知
利用“错位相减法”即得
试题解析:(Ⅰ)由题意当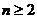
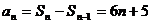
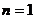
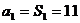
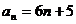
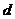
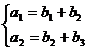
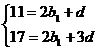

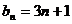
(Ⅱ)由(Ⅰ)知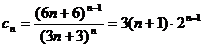
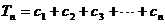
,所以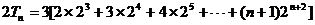
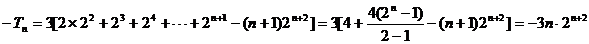
所以
考查方向
知识点
4.已知





正确答案
解析
考查方向
解题思路
本题属于常规题,使用直接法,计算找出规律,分组求和,
易错点
该题易错于无法找到数列的规律性
知识点
15.已知数列




正确答案
解析



考查方向
解题思路
本题考查转化思想的能力,解题步骤如下:将


易错点
不会转化成关于和有关的式子。
知识点
18. 已知正项数列







正确答案
见解析
解析
试题分析:本题属于数列中的基本问题,题目的难度是逐渐由易到难.
(1)由题意知:①当n=1时,∵2S1=
∴
②当n≥2时,
∴
∴
∴ 数列
∴
(2)由(1)知
∴
∴
相减得

∴ 
考查方向
解题思路
本题考查数列问题,解题步骤如下:1、利用an与Sn的关系求解。2、利用等比数列的求和公式求解。
易错点
等比数列分项时项数易错。
知识点
19. 设数列




(I)求数列

(II)将数列






正确答案
(1)
解析
试题分析:本题属于数列中的基本问题,题目的难度是逐渐由易到难.
(1)由已知得
(2)由已知得:

首项分别是

T2006=(c1+c3+……+c2015)+(c2+……+c2016)=
考查方向
解题思路
本题考查数列问题,解题步骤如下:
1、利用an与Sn的关系求解。
2、利用等比数列的求和公式求解。
易错点
等比数列分项时项数易错。
知识点
7. 数列{an}的通项公式an=ncos,其前n项和为Sn,则S2016等于( )
正确答案
解析
其中所有的奇数项都为0,而偶数项是分别为第二项是-2,第四项是4,第六项是-6,第八项是8,这样可以将每2项相加放在一起,刚好有1008个偶数项,即可以组成504组,每组的值为2,所有答案就为1008,故A正确。
考查方向
解题思路
算出前4项并找到这个数列的规律,最后用求和公式解决。
易错点
1、不能找到数列的周期性,没有找到规律导致无法计算下去。
知识点
13.若数列


正确答案
28
解析
由于
考查方向
解题思路
将连续两项看成是一项,就可以构造出一个等差数列。
易错点
公差是4的数列。
知识点
18. 已知数列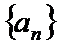
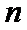
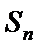
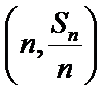
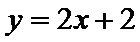
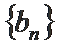
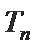
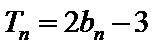
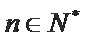
(Ⅰ)求数列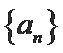
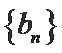
(Ⅱ)设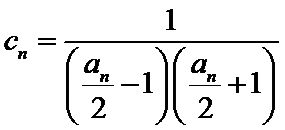
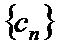
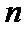
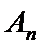
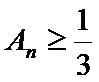
正确答案
(1)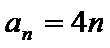
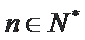
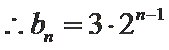
解析
试题分析:本题属于数列中的基本问题,题目的难度是逐渐由易到难.
解:(Ⅰ)由题意,得 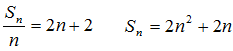
当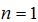
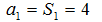
当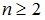
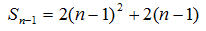
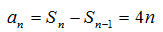
综上,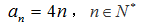
又
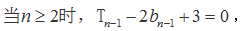
数列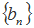
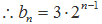
(Ⅱ)
考查方向
解题思路
本题考查数列问题,解题步骤如下:
1、利用an与Sn的关系求解。
2、利用等比数列的求和公式求解。
易错点
等比数列分项时项数易错。
知识点
18. 设数列

(1)求数列

(2)是否存在正整数n,使得
正确答案
(1)
(2)
解析
本题属于三角函数的图像与性质及正余弦定理的综合应用问题,属于简单题,只要掌握相关函数的知识,即可解决本题,解析如下:
解:(1)
所以
两式相减得:
即

所以

所以
所以
所以
所以
所以

考查方向
本题考查了数列的相关知识点,属于简单题。
易错点
相关知识点不熟悉导致出错。
知识点
19. 设数列






(1)求证:数列

(2)令








正确答案
见解析
解析
解:(1)当


代入

而
∴数列
∴


又
(2)当



∴
故
当

若
则等式


若


∵



∴当且仅当


综上可知,当


当


考查方向
解题思路
利用

易错点
忽略n的范围的讨论。
知识点
扫码查看完整答案与解析