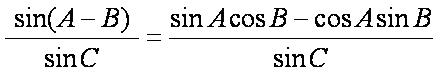- 弦切互化
- 共25题
1
题型:简答题
|
已知向量

(1)求 tanA的值;
(2)求函数
正确答案
见解析。
解析
(1)m·n=sinA-2cosA=0,得tanA=2.
(2)
当

所以f(x)的值域是
知识点
正弦函数的定义域和值域弦切互化三角函数中的恒等变换应用数量积判断两个平面向量的垂直关系
1
题型:
单选题
|
定义:设W是由一平面内的n(n≥3)个向量组成的集合。若a
中除a外的所有向量和的模,则称a是W的极大向量,下列命题:
①若W中每个向最量方向都相同,则W中必存在一个极大向最;
②给定平面内两个不共线向里a、b,在该平面内总存在唯一的平面向里c,使得
W={a,b,c}中的每个元索都是极大向jg ;
③若

一个元素也都是极大向量,其中真命题的个数是
正确答案
B
解析
略
知识点
弦切互化
1
题型:简答题
|
在△ABC中,已知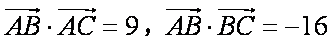
(1)AB的值;
(2)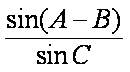
正确答案
见解析。
解析
(1)(方法1)因为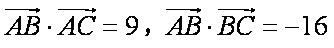
所以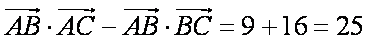
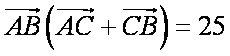
亦即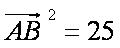

(方法2)设A,B,C的对边依次为a,b,c,
则由条件得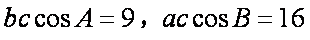
两式相加得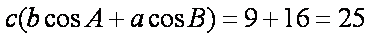
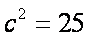
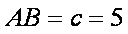
(方法3)设A,B,C的对边依次为a,b,c,
则由条件得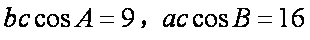
由余弦定理得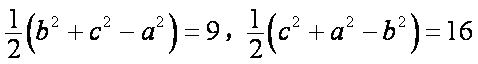
两式相加得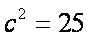
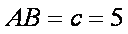
(2)
由正弦定理得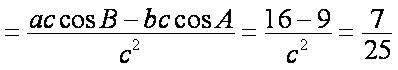
知识点
弦切互化
1
题型:填空题
|
已知










正确答案
解析
,由正弦定理




知识点
弦切互化
1
题型:简答题
|
(1)已知

(2)化简
正确答案
见解析。
解析
(1)

(2)



知识点
同角三角函数间的基本关系弦切互化运用诱导公式化简求值
下一知识点 : 三角函数中的恒等变换应用
扫码查看完整答案与解析