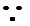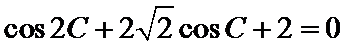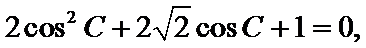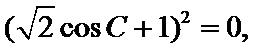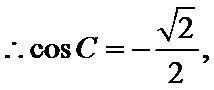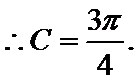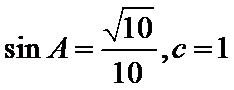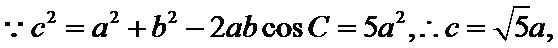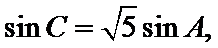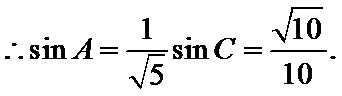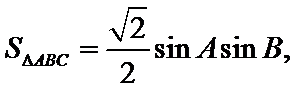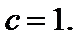- 余弦定理的应用
- 共46题
已知



17.若

18.若


正确答案
解析
试题分析:本题属于三角恒等变形和解三角形的基本问题,对

又


考查方向
解题思路
本题考查解三角形,解题步骤如下:对

易错点
对

正确答案

解析
试题分析:本题属于三角恒等变形和解三角形的基本问题,由方程思想求解出边长再算出面积;由17可知






考查方向
解题思路
本题考查解三角形,解题步骤如下:由方程思想求解出边长再算出面积。
易错点
根据条件合理选择定理来解三角形。
在




16.求
17.若


正确答案

解析
试题分析:本题属于向量的坐标运算、正余弦定理及三角形的面积公式的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:因为





考查方向
解题思路
利用向量

易错点
相关知识点不熟容易处错。
正确答案

解析
试题分析:本题属于向量的坐标运算、正余弦定理及三角形的面积公式的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
由余弦定理得,
化简得,




故

考查方向
解题思路
利用余弦定理求出a边,在利用面积公式即可求出

易错点
相关知识点不熟容易处错。
在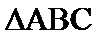
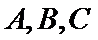
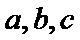
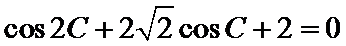
16.求角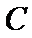
17.若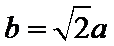
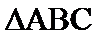

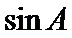

正确答案
(1) 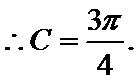
解析
(Ⅰ)
即
又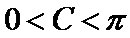
考查方向
解题思路
根据题中给出等式求出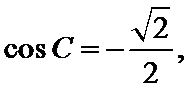
易错点
对于正弦定理的反复转化不明白。
正确答案
(2)
解析
(Ⅱ)
由正弦定理,得
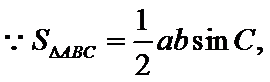
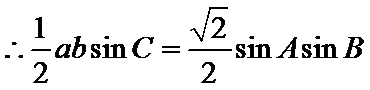
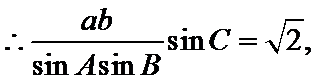
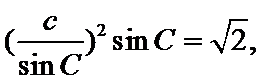
考查方向
解题思路
先根据余弦定理求出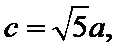
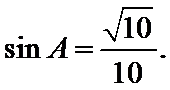
易错点
不知道该如何使用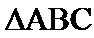
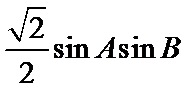
在教育宗旨问题上,梁启超主张通过教育培养
A.政治家
B.学术人才
C.新国民
D.实业人才
正确答案
C
解析
[分析] 本题旨在考查考生对中国近代维新派教育家及其代表人物教育思想贡献及其历史意义的掌握程度。维新派教育家的思想贡献在于首先明确提出普及教育的主张和培养具有时代人格精神的国民,这是他们区别于洋务派教育思想之处。尽管他们不排斥培养政治家、学术人才和实业人才,但其着眼点显然不在于此。故本题正确答案为C。
16.如图,在





正确答案
解析
解题思路
教师点评
知识点
16.在





正确答案
知识点
扫码查看完整答案与解析