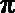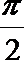- 函数的概念与基本初等函数
- 共5812题
10.定义:若函数







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.当点(x,y)在函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知a是函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.如果函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设

(1)讨论函数
(2)已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数
(I)求
(II)若在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.选考题:请考生在第1、2、3题中任选一题做答,如果多做,则按所做的第一题记分。
1.如图,







(1)
(2)
2.在直角坐标系中,以原点为极点,








(1)写出曲线

(2)若

3.已知函数


(1)求
(2)解关于

正确答案
1.
证明:(1)因为

又已知


而


故


(2)因为


而
故
2.
(1)C:
(2)将直线的参数表达式代入抛物线得

3.
(1)∵
∴
(2)当

当

当

综上:此不等式的解集为
解析
解析已在路上飞奔,马上就到!
知识点
8.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.下列函数中,定义域是
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数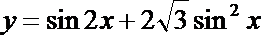

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18、某种产品的广告费支出x与销售额y(单位:万元)之间有如下对应数据:
(1)求回归直线方程;
(2)试预测广告费支出为10万元时,销售额多大?
(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率。(参考数据: 
正确答案
(1)



因此,所求回归直线方程为:
(2)根据上面求得的回归直线方程,当广告费支出为10万元时,
(3)
基本事件:(30,40),(30,60),(30,50),(30,70),(40,60),(40,50),(40,70),(60,50),(60,70),(50,70)共10个,
两组数据其预测值与实际值之差的绝对值都超过5的有(60,50),
所以至少有一组数据其预测值与实际值之差的绝对值不超过5的概率为
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析