圆的一般方程
共16题

· 圆的一般方程

圆的一般方程
共16题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

15.设直线y=x+2a与圆C：x2+y2-2ay-2=0相交于A，B两点，若，则圆C的面积为 .

正确答案

知识点

圆的标准方程圆的一般方程

题型：简答题

简答题 · 16 分

18．如图，在平面直角坐标系中，设点是椭圆上一点，从原点向圆作两条切线分别与椭圆交于点，直线的斜率分别记为.

（1）若圆与轴相切于椭圆的右焦点，求圆的方程；

（2）若.

①求证：；

②求的最大值.

正确答案

（1）圆的方程为.（2）详见解析

解析

试题分析：本题属于直线与圆锥曲线的综合问题，题目的难度较大，（1）直接求圆心和半径（2）证明定值问题时，要先表示出来，再通过计算化简得到（3）的最大值涉及到基本不等式，要能正确地使用基本不等式。

（1）因为椭圆右焦点的坐标为，所以圆心的坐标为，

从而圆的方程为.

（2）①因为圆与直线相切，所以，

即，

同理，有，

所以是方程的两根，

从而.

②设点，联立，

解得，

同理，，

所以

，当且仅当时取等号. 所以的最大值为.

考查方向

本题考查了椭圆的方程，直线与圆的位置关系，直线与椭圆的位置关系。

解题思路

本题考查直线与圆锥曲线的位置关系，解决直线与椭圆的位置关系的相关问题时，常规思路是先把直线与椭圆联立方程组，消元、化简，然后应用根与系数的关系代入化简，从而解决相关问题。

易错点

1、第二问中证明，计算不出来常数。

2、第三问中求时，计算错误，同时使用基本不等式时有一定的难度。

知识点

圆的一般方程圆锥曲线中的范围、最值问题圆锥曲线的定点、定值问题直线、圆及圆锥曲线的交汇问题

题型：填空题

填空题 · 5 分

12．若点在以坐标原点为圆心的圆上，则该圆在点P处的切线方程为________.

正确答案

解析

由点在以坐标原点为圆心的圆上知此圆的方程为：，所以该圆在点P处的切线方程为即，故填：.

考查方向

本题主要考查直线和圆相切的性质，属于基础题．.

解题思路

本题考查复数的概念和运算，采用分母实数化和利用共轭复数的概念进行化解求解.

易错点

本题属于基础题，注意运算的准确性

知识点

圆的一般方程圆的切线方程

题型：填空题

填空题 · 5 分

15.已知直线：与圆交于两点，过分别作的垂线与轴交于两点，则_____________.

正确答案

解析

由，得，代入圆的方程，并整理，得，

从而可得。又直线l的倾斜角为，由平面几何知识知，在梯形ABCD中，

考查方向

本题主要考查了直线与圆的位置关系等知识，为高考题的必考题，在近几年的各省高考题出现的频率较高

解题思路

由，得，代入圆的方程，再由平面几何知识知，在梯形ABCD中，

易错点

对直线与圆的位置关系理解出现错误、计算错误

知识点

圆的一般方程

题型：填空题

填空题 · 5 分

15.直线l：与x轴、y轴分别相交于点A、B，O为坐标原点，则△OAB的内切圆的方程为____．

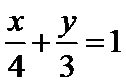
正确答案

(x－1)2 ＋(y－1)2＝1

解析

设△OAB的内切圆的方程为，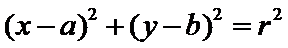

由题意得，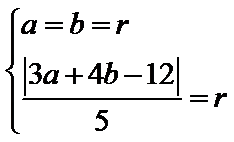

解得或，由于，所以舍去，

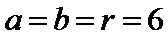
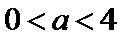
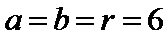
故所求圆的方程为(x－1)2 ＋(y－1)2＝1 。

考查方向

本题主要考查圆的方程的求法，意在考查考生的数形结合能力和运算求解能力。

解题思路

1.先利用待定系数法设出圆的方程；

2.根据圆与三角形的各边均相切列出方程组，求出内切圆的方程。

易错点

1.无法根据题意射出圆的方程，感觉无从下手；

2.处理数据出错导致答案不正确。

知识点

圆的一般方程直线与圆的位置关系

题型：填空题

填空题 · 5 分

12.已知圆C的圆心坐标为，抛物线的准线被圆C截得的弦长为2，则圆C的方程为_________；

正确答案

解析

根据抛物线几何性质可知准线方程，则圆心到直线的距离，根据相交弦公式

所以圆的标准方程为

考查方向

本题主要考察了抛物线的几何性质，考察了直线与圆相交的性质，考察了直线和圆的相交弦问题，考察了圆的标准方程

解题思路

该题思路比较清晰，主要有以下几个步骤1、写出准线方程2、求出圆心到直线的距离3、利用相交弦公式求出半径4、带入求出圆的标准方程

易错点

本题易错点主要集中在准线的表达，弦长公式的表达

知识点

圆的一般方程直线与圆相交的性质抛物线的标准方程和几何性质直线、圆及圆锥曲线的交汇问题

棒棒哒，已学完当前知识点学习下一知识点

下一知识点 : 轨迹方程的问题

百度题库 > 高考 > 文科数学 > 圆的一般方程

扫码查看完整答案与解析