- 指数函数的定义、解析式、定义域和值域
- 共5题
请考生从下面三道大题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号
(1)如图O是等腰三角形ABC内一点,圆O与△ABC的底边BC交于M,N两点,与底边上的高交于点G,且与AB,AC分别相切于E,F两点.(请回答27、28题)
(2)在直角坐标系




(3)设

27.证明
28.若AG等于圆O半径,且
29.求

30.若




31.若

32.

正确答案
由于











正确答案
28.若AG等于圆O半径,且

解析
试题分析:通过AD是∠CAB的角平分线及圆O分别与AB、AC相切于点E、F,利用相似的性质即得结论.
由于











考查方向
解题思路
平面几何中平行关系的证明往往有三种方法:①由垂直关系得出;②由角的关系得出;③由平行关系的传递性得出.
易错点
边角关系的准确把握
正确答案


解析
试题分析:由曲线C2:ρ=2sinθ,化为ρ2=2ρsinθ,把
曲线










考查方向
解题思路
将曲线

易错点
参数方程及极坐标方程转化普通方程
正确答案

解析
试题分析:由曲线C1的参数方程,消去参数t,化为普通方程:y=xtanα,其中0≤α≤π,其极坐标方程为:θ=α(ρ∈R,ρ≠0),利用
曲线










考查方向
解题思路
分别联立





易错点
三角函数公式的灵活运用
正确答案
因为





解析
试题分析:运用不等式的性质,结合条件a,b,c,d均为正数,且a+b=c+d,ab>cd,即可得证.
因为





考查方向
解题思路
要证明

易错点
不等式性质的正确应用.
正确答案
从两方面证,①若
















解析
详见答案.
考查方向
解题思路
充要条件的证明需要分为两步,即充分条件的证明和必要条件的证明.证明的关键是寻找条件和结论以及它们和已知之间的联系.
易错点
充要条件的证明一定要分两步进行,及必要性与充分性的证明.
1.集合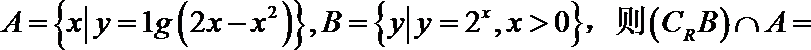
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数

(1)求
(2)求
(3)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
设函数
26.求曲线

27.设

28.求证:

正确答案
由

因为

所以曲线


考查方向
解题思路
(1)利用导数的几何意义计算(2)利用极值与单调性计算
易错点
有三个零点时一定要检验
正确答案
当

所以
令






所以,当





由


考查方向
解题思路
(1)利用导数的几何意义计算(2)利用极值与单调性计算
易错点
有三个零点时一定要检验
正确答案
当


此时函数


当


当



当



所以
综上所述,若函数

故

当



所以

因此

考查方向
解题思路
(1)利用导数的几何意义计算(2)利用极值与单调性计算
易错点
有三个零点时一定要检验
若函数


正确答案
解析
当






知识点
扫码查看完整答案与解析