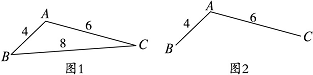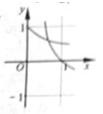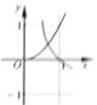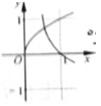指数函数的图像与性质
共51题

指数函数的图像与性质
共51题

热门试卷

题型：填空题

填空题 · 5 分

某地区规划道路建设，考虑道路铺设方案，方案设计图中，点表示城市，两点之间连线表示两城市间可铺设道路，连线上数据表示两城市间铺设道路的费用，要求从任一城市都能到达其余各城市，并且铺设道路的总费用最小，例如：在三个城市道路设计中，若城市间可铺设道路的线路图如图1，则最优设计方案如图2，此时铺设道路的最小总费用为10。

现给出该地区可铺设道路的线路图如图3，则铺设道路的最小总费用为__________。

正确答案

解析

由题意知，各城市相互到达，且费用最少为1＋2＋2＋3＋3＋5＝16＝FG＋GD＋AE＋EF＋GC＋BC

知识点

指数函数的图像与性质

题型：单选题

单选题 · 5 分

已知函数若有则的取值范围为

正确答案

解析

由题可知，，若有则，即，解得。

知识点

指数函数的图像与性质

题型：单选题

单选题 · 5 分

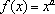
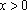
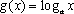
在同一直角坐标系中，函数（），的图象可能是（）

正确答案

解析

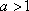
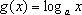
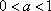
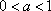
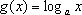
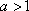
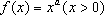
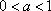
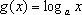
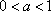
对A，没有幂函数的图象，；对B,中，中，不符合题题；对C，中，中，不符合题题；对D，中，中，符合题题；故选D. 点评：本题考查幂函数与对数函数的图象判断，容易题

知识点

指数函数的图像与性质对数函数的图像与性质反函数函数图象的应用

题型：简答题

简答题 · 16 分

设函数的定义域为，值域为，如果存在函数，使得函数的值域仍然是，那么，称函数是函数的一个变换.

（1）判断函数是不是，的一个变换？说明你的理由；

（2）设的值域，已知是的一个变换，且函数的定义域为，求实数的值；

（3）设函数的定义域为，值域为，函数的定义域为，值域为，写出是的一个变换的充分非必要条件（不必证明）。

正确答案

见解析

解析

（1）函数的值域为，

，

所以，不是的一个变换；

（2）的值域为，由知，

即定义域为，

因为是的一个变换，且函数的定义域为，

所以，的值域为，

，

所以，恒有，且存在使两个等号分别成立，

于是，解得或

（3）设函数的定义域为，值域为，函数的定义域为，值域为，则是的一个变换的充分非必要条件是“=”。

条件的不必要性的一个例子是。

，，，，

此时，但的值域仍为，

即是的一个等值域变换。（反例不唯一）

知识点

指数函数的图像与性质

题型：单选题

单选题 · 5 分

若，则的大小顺序是（）

正确答案

解析

略。

知识点

指数函数的图像与性质对数值大小的比较不等式的基本性质比较法

继续学习学习下一知识点

下一知识点 : 指数函数的图像变换

百度题库 > 高考 > 文科数学 > 指数函数的图像与性质

扫码查看完整答案与解析