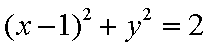- 直线与圆的位置关系
- 共93题
4.“C=5”是“点(2,1)到直线3x+4y十C=0的距离为3”的( )
正确答案
解析
由题意知点







考查方向
解题思路
先求出点(2,1)到直线3x+4y十C=0的距离为3的充要条件的C的值为

易错点
采用代入验证出错。
知识点
14. 已知圆





正确答案
解析
当直线












考查方向
解题思路
讨论直线

易错点
本题易在求
知识点
如图,在平面直角坐标系xoy中,椭圆

26.求椭圆的方程;
27.若直线AB斜率为1时,求弦AB长;
28.过椭圆的对称中心O,作直线L,交椭圆与M,N,三角形FMN是否存在在大面积?若存在,求出它的最大面积值。若不存在,说明理由
正确答案
当AB的斜率为0时,AB=半长轴,即
2a=4,a=2;
又因为 e=c/a,
又
所以解析式为
解析
看解题步骤
考查方向
圆锥曲线
解题思路
利用离心率公式。abc之间的关系
易错点

教师点评
考查圆锥曲线解析式求解
正确答案
联立直线与椭圆方程得:5x2-8x=0设方程根为x1=0,x2=8/5,
|AB|=
解析
见答案
考查方向
直线与圆锥曲线的关系,两点之间的距离
解题思路
先求出两焦点的横坐标,利用距离与斜率、求两点间的距离公式求解
易错点
无
教师点评
考查了直线与圆锥曲线的关系,和用斜率求两点距离
正确答案
S⊿FMN= 

10.在平面直角坐标系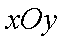
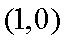
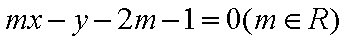
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析