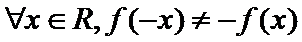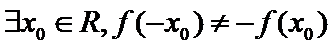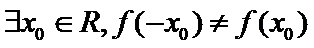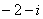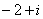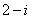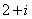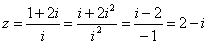- 函数单调性的判断与证明
- 共139题
3.设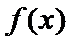
正确答案
考查方向
解题思路
1.先根据奇函数的定义得到题中命题的逆否命题;
易错点
1.全称命题的否定形式写错;2.不能正确理解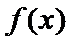
知识点
已知函数f(x)=x3+ax2+b(a,b∈R).
25.试讨论f(x)的单调性;
26.若b=c﹣a(实数c是与a无关的常数),当函数f(x)有三个不同的零点时,a的取值范围恰好是(﹣∞,﹣3)∪(1,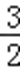
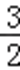
正确答案
函数f(x)在(﹣∞,0),(﹣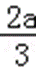
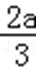
解析
(1)∵f(x)=x3+ax2+b,
∴f′(x)=3x2+2ax,
令f′(x)=0,可得x=0或﹣
a=0时,f′(x)>0,∴f(x)在(﹣∞,+∞)上单调递增;
a>0时,x∈(﹣∞,﹣

∴函数f(x)在(﹣∞,﹣
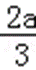
a<0时,x∈(﹣∞,0)∪(﹣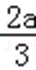
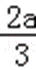
∴函数f(x)在(﹣∞,0),(﹣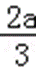
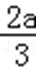
考查方向
解题思路
(1)求导数,分类讨论,利用导数的正负,即可得出f(x)的单调性;
易错点
本题考查导数知识的综合运用,考查函数的单调性,分类讨论中易错
正确答案
c=1
解析
(2)由(1)知,函数f(x)的两个极值为f(0)=b,f(﹣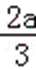
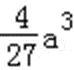
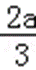
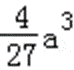
∵b=c﹣a,
∴a>0时,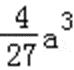
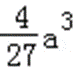
设g(a)=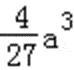
∵函数f(x)有三个不同的零点时,a的取值范围恰好是(﹣∞,﹣3)∪(1,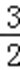
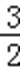
∴在(﹣∞,﹣3)上,g(a)<0且在(1,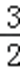
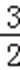
∴g(﹣3)=c﹣1≤0,且g(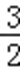
∴c=1,
此时f(x)=x3+ax2+1﹣a=(x+1)[x2+(a﹣1)x+1﹣a],
∵函数有三个零点,
∴x2+(a﹣1)x+1﹣a=0有两个异于﹣1的不等实根,
∴△=(a﹣1)2﹣4(1﹣a)>0,且(﹣1)2﹣(a﹣1)+1﹣a≠0,
解得a∈(﹣∞,﹣3)∪(1,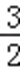
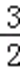
综上c=1.
考查方向
解题思路
(2)由(1)知,函数f(x)的两个极值为f(0)=b,f(﹣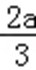
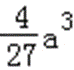
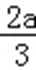
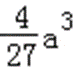
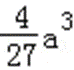
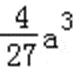
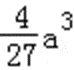
易错点
本题考查导数知识的综合运用,考查函数的单调性,考查函数的零点,在用范围的过程中易错.
已知函数f(x)=x3+ax2+b(a,b∈R).
25.试讨论f(x)的单调性;
26.若b=c﹣a(实数c是与a无关的常数),当函数f(x)有三个不同的零点时,a的取值范围恰好是(﹣∞,﹣3)∪(1,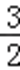
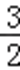
正确答案
函数f(x)在(﹣∞,0),(﹣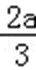
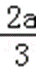
解析
(1)∵f(x)=x3+ax2+b,
∴f′(x)=3x2+2ax,
令f′(x)=0,可得x=0或﹣
a=0时,f′(x)>0,∴f(x)在(﹣∞,+∞)上单调递增;
a>0时,x∈(﹣∞,﹣

∴函数f(x)在(﹣∞,﹣
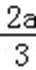
a<0时,x∈(﹣∞,0)∪(﹣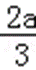
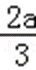
∴函数f(x)在(﹣∞,0),(﹣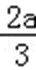
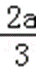
考查方向
解题思路
(1)求导数,分类讨论,利用导数的正负,即可得出f(x)的单调性;
易错点
本题考查导数知识的综合运用,考查函数的单调性,分类讨论中易错
正确答案
c=1
解析
(2)由(1)知,函数f(x)的两个极值为f(0)=b,f(﹣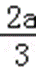
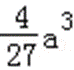
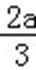
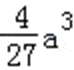
∵b=c﹣a,
∴a>0时,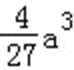
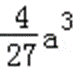
设g(a)=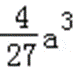
∵函数f(x)有三个不同的零点时,a的取值范围恰好是(﹣∞,﹣3)∪(1,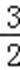
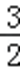
∴在(﹣∞,﹣3)上,g(a)<0且在(1,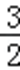
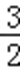
∴g(﹣3)=c﹣1≤0,且g(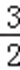
∴c=1,
此时f(x)=x3+ax2+1﹣a=(x+1)[x2+(a﹣1)x+1﹣a],
∵函数有三个零点,
∴x2+(a﹣1)x+1﹣a=0有两个异于﹣1的不等实根,
∴△=(a﹣1)2﹣4(1﹣a)>0,且(﹣1)2﹣(a﹣1)+1﹣a≠0,
解得a∈(﹣∞,﹣3)∪(1,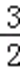
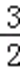
综上c=1.
考查方向
解题思路
(2)由(1)知,函数f(x)的两个极值为f(0)=b,f(﹣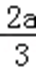
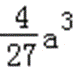
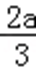
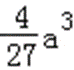
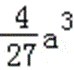
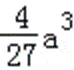
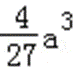
易错点
本题考查导数知识的综合运用,考查函数的单调性,考查函数的零点,在用范围的过程中易错.
已知函数
25.求函数
26.若函数






27.求证:
正确答案
详见解析
解析
解:(Ⅰ)由

①当




所以此时


②当



③当

考查方向
利用导数求函数的单调区间
解题思路
先求导,然后利用导数来求函数的单调区间
易错点
求导错误,分类讨论错误
教师点评
导数大于0时,原函数单调递增
导数小于0是,原函数单调递减
正确答案
详见解析
解析
(Ⅱ)由题知

所以
所以


∵


又∵
不妨设




即



于是只需

考查方向
函数与导数相结合问题,利用导数求方程根的分布情况及个数
解题思路
求导,然后另导函数的值为0,判断导函数的根的情况,进而判断出原函数的根的分布特点。
正确答案
详见解析
解析
(Ⅲ)由(Ⅰ)知当


∴
在上式中分别令
得
以上不等式相乘
得
两边同除以
得

考查方向
函数与不等式综合题,利用导数证明不等式成立
解题思路
先判断函数的单调性,利用单调性证明不等式
易错点
构造函数错误,计算化简能力弱
教师点评
此题关键在于如何构造正确的函数
影响基金类产品收益的因素有两方面,其中来自基金自身的因素有( )。
A.货币市场工具
B.基金管理公司的整体业务运行情况
C.基金管理人员的业务素质
D.股票和债券
E.基金管理公司的资产管理与投资策略
正确答案
B,C,E
解析
[解析] 选项AD是来自基金基础市场的因素,所以不选。
13. 函数



正确答案
解析
:∵当-1≤x≤1时,|f(x)|≤1恒成立,
∴-1≤f(0)=n≤1,-1≤f(1)=n+2≤1,
∴n=-1,
∴-1≤f(-1)=2m-3≤1,即1≤m≤2,
当对称轴x=0,且f(0)=-1,满足条件
∴m=2,∴f(x)=2x2-1
所以
考查方向
二次函数的性质,函数的性质及应用
解题思路
首先,根据二次函数的图象与性质,其对称轴x=0,且f(0)=-1,得到m=2,n=-1,然后求解
易错点
对函数的性质掌握不好
知识点
若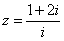
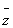
正确答案
解析
知识点
12.设函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合


正确答案
解析
略
知识点
2.复数

正确答案
解析
略
考查方向
象限
解题思路
象限
易错点
象限
知识点
扫码查看完整答案与解析