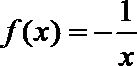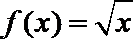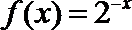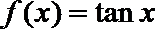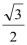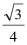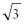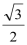- 函数单调性的判断与证明
- 共139题
13. 函数y=-(x-3)|x|的递减区间是__________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数
①函数的定义域为
②

③

④

写出满足上述性质的一个函数为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.函数y=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.“


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.下列函数中,在定义域内是减函数的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设
(1)求

(2)讨论

(3)令





正确答案
(1)
(2)设
∴







(3)当


∴










解析
解析已在路上飞奔,马上就到!
知识点
12.如图是函数




正确答案

解析
解析已在路上飞奔,马上就到!
知识点
7.已知△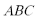
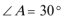
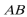
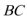
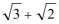

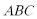
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数
(1)求
(2)请讨论它的单调性,并给予证明。
正确答案
(1)

即


经验证当

(2)先研究
得

由于

解析
解析已在路上飞奔,马上就到!
知识点
12. 已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析