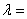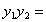抛物线及其性质
共383题

抛物线及其性质
共383题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

设为抛物线上一点，为抛物线的焦点，若以为圆心，为半径的圆和抛物线的准线相交，则的取值范围是（）

正确答案

解析

略

知识点

抛物线的定义及应用

题型：填空题

填空题 · 5 分

已知抛物线上一点到焦点的距离是，则点的坐标是_____，

正确答案

解析

略

知识点

抛物线的定义及应用

题型：简答题

简答题 · 14 分

已知椭圆的左右焦点为，抛物线C：以为焦点。

（1）求抛物线的标准方程；

（2）设、是抛物线上两动点，过点的直线，与轴交于点、. 是以、为腰的等腰三角形，探究直线的斜率是否为定值？若是求出这个定值，若不是说明理由.

正确答案

见解析。

解析

（1）由椭圆方程得半焦距

所以椭圆焦点为

又抛物线C的焦点为

（2）直线AB的斜率为定值—1.

证明如下：设，，，A、B在抛物线上，

由①-③得，

由②-③得，

因为是以MP,MQ为腰的等腰三角形，所以

由得化简整理，

得

由得：

为定值

解法二：设，

则，

因为是以MP,MQ为腰的等腰三角形，所以

即

所以

所以，由得

所以，

所以，直线AB的斜率为定值，这个定值为

知识点

抛物线的定义及应用

题型：简答题

简答题 · 14 分

已知椭圆和抛物线有公共焦点, 的中心和的顶点都在坐标原点，直线过点.

（1）写出抛物线的标准方程；

（2）若坐标原点关于直线的对称点在抛物线上，直线与椭圆有公共点，求椭圆的长轴长的最小值.

正确答案

见解析。

解析

（1）

由题意，抛物线的焦点，则

所以方程为：，

（2）解法1、

设，则中点为，

因为两点关于直线对称，所以

即，解之得，

将其代入抛物线方程，得：，所以

联立，消去，得：

由，得，

注意到，即，所以，即，

因此，椭圆长轴长的最小值为.

解法2

设，因为两点关于直线对称，则，

即，解之得

即,根据对称性,不妨设点在第四象限，且直线与抛物线交于

如图

.则,于是直线方程为

联立，消去，得：

由，得，

注意到，即，所以，即，

因此，椭圆长轴长的最小值为.

知识点

抛物线的定义及应用

题型：填空题

填空题 · 5 分

以抛物线上的点为圆心，并过此抛物线焦点的圆的方程是（） .

正确答案

解析

略

知识点

抛物线的定义及应用

题型：单选题

单选题 · 5 分

过抛物线的焦点F，斜率为的直线交抛物线于A，B两点，若，则的值为

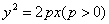
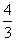
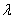
正确答案

解析

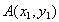
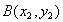
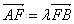
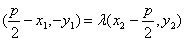
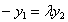
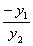
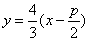
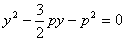
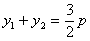
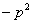
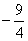
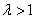
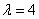
根据题意设，，由得，故，即，设直线AB的方程为，联立直线与抛物线方程，消元得，故，，，即，又，故。

知识点

抛物线的定义及应用

题型：填空题

填空题 · 5 分

已知点是抛物线上的点，设点到抛物线准线的距离为，到圆上的一动点的距离为，则的最小值是。

正确答案

解析

略

知识点

抛物线的定义及应用

题型：单选题

单选题 · 5 分

已知抛物线的焦点为F，是抛物线C上的不同三点，且、、成等差数列，公差，若点的横坐标为3，则线段的垂直平分线与x轴交点的横坐标是

D不确定，与d的值有关

正确答案

解析

略

知识点

抛物线的定义及应用

题型：简答题

简答题 · 14 分

已知椭圆，点在椭圆上。

（1）求椭圆的离心率；

（2）设为椭圆的右顶点，为坐标原点，若在椭圆上且满足求直线的斜率的值。

正确答案

见解析。

解析

解：(1) 点在椭圆上

(2) 法一：由(1)得,，椭圆方程为：

设满足条件，则：……………①

由得：……………②

由①②得：

解得：（舍），

故（13分）

直线的斜率（

法二：设；

则

（8分）

（10分），（

直线的斜率

知识点

抛物线的定义及应用

题型：单选题

单选题 · 5 分

若抛物线的焦点与双曲线的右焦点重合，则的值为

正确答案

解析

略

知识点

抛物线的定义及应用

继续学习学习下一知识点

下一知识点 : 直线与圆锥曲线的位置关系

百度题库 > 高考 > 文科数学 > 抛物线及其性质

扫码查看完整答案与解析