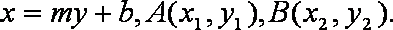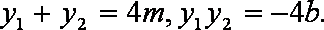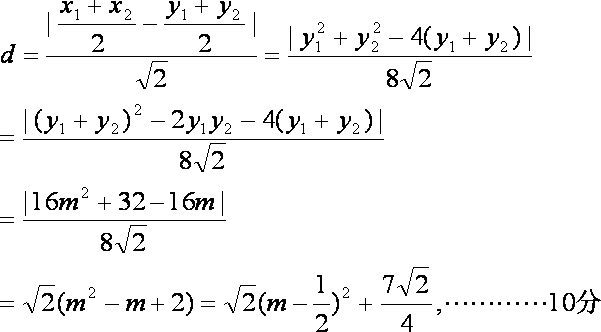- 抛物线及其性质
- 共383题
已知抛物线

正确答案
解析
略
知识点
已知抛物线
(1)若直线


(2)设A,B为抛物线上两点,且A
正确答案
见解析。
解析
(1)由已知,x=4不合题意。设直线L的方程为
由已知,抛物线C的焦点坐标为(1,0), ………………1分
因为点F到直线l的距离为2,所以

解得

所以直线l的方程为
(2)设A、B坐标为A(

因为AB不垂直于x轴,设直线AB的方程为

联立方程


因为AB中点的横坐标为2,故
整理得
由AB中点的坐标为(2,2k+b)
得AB垂直平分线的方程为:
将

线段AB的垂直平分线恰过定点(4,0) …………………14分
知识点
P为抛物线

正确答案
解析
焦点



知识点
过抛物线y2=2px(p>0)的对称轴上的定点M(m,0)(m>0),作直线AB与抛物线相交于A,B两点。
(1)试证明A,B两点的纵坐标之积为定值;
(2)若点N是定直线l:x=﹣m上的任一点,试探索三条直线AN,MN,BN的斜率之间的关系,并给出证明。
正确答案
见解析
解析
(1)证明:,设A(x1,y1),B(x2,y2)有y1•y2=﹣2pm,下证之:
设直线AB的方程为:x=ty+m,与y2=2px联立
消去x得y2﹣2pty﹣2pm=0,
由韦达定理得y1•y2=﹣2pm,
(2)解:三条直线AN,MN,BN的斜率成等差数列,下证之:
设点N(﹣m,n),则直线AN的斜率为
直线BN的斜率为
∴
=
=
又∵直线MN的斜率为
∴kAN+kBN=2kMN
即直线AN,MN,BN的斜率成等差数列。
知识点
设点








(1)若抛物线




(2)当


(3)若将题设中的抛物线方程

正确答案
见解析
解析
(1)解:抛物线






∴ 
(2)证明:由




即
则

(3)经推广的命题:
“当


其逆命题为:
“当


该逆命题为假命题。
不妨构造特殊化的一个反例:
设




根据抛物线的定义得:

不妨取四点坐标分别为




所以逆命题是假命题。
知识点
设抛物线





(1)求抛物线
(2)过点





(3)设







正确答案
见解析
解析
(1)由条件得


……………………………. 4分
(2)直线方程为


……………………………. 6分



………


(3)设所作直线的方向向量为

得


……………………………. 12分
又



即


因此
……………………………. 17分
又

……………………………. 18分
知识点
已知抛物线C:



(1)求抛物线C的焦点坐标;
(2)若抛物线C上有一点

(3)是否存在实数m,使△ABQ是以Q为直角顶点的直角三角形?若存在,求出m 的值;若不存在,说明理由。
正确答案
见解析。
解析
(1)∵抛物线





(3)联立方程



则






得
若存在实数



即


即






知识点
已知A、B是抛物线
(1)求证:直线AB过定点M(4,0);
(2)设弦AB的中点为P,求点P到直线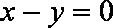
正确答案
见解析。
解析
(1)设直线AB方程为
将直线AB方程代入抛物线方程

(2)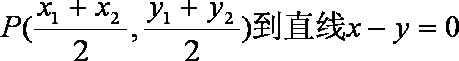
当
知识点
抛物线













(1)求
(2)证明:
(3)







正确答案
见解析
解析
(1)


(2)

A(








所以直线AC和直线AB的倾斜角互补, 
(3)设
则m=n=|AD|sin



把








知识点
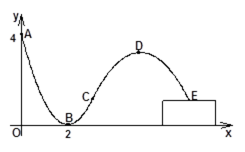
轮滑是穿着带滚轮的特制鞋在坚硬的场地上滑行的运动,如图,助跑道ABC是一段抛物线,某轮滑运动员通过助跑道获取速度后飞离跑道然后落到离地面高为1米的平台上E处,飞行的轨迹是一段抛物线CDE(抛物线CDE与抛物线ABC在同一平面内),D为这段抛物线的最高点,现在运动员的滑行轨迹所在平面上建立如图所示的直角坐标系,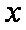
(1)求助跑道所在的抛物线方程;
(2)若助跑道所在抛物线与飞行轨迹所在抛物线在点C处有相同的切线,为使运动员安全和空中姿态优美,要求运动员的飞行距离在4米到6米之间(包括4米和6米),试求运动员飞行过程中距离平台最大高度的取值范围?
正确答案
见解析
解析
解:(1)设助跑道所在的抛物线方程为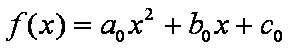
依题意: 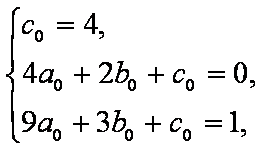
解得,
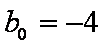

∴助跑道所在的抛物线方程为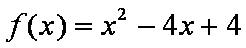
(2)设飞行轨迹所在抛物线为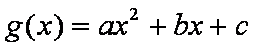
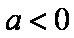
依题意: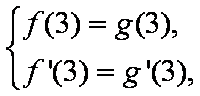

∴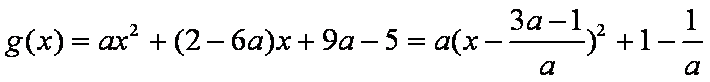
令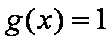
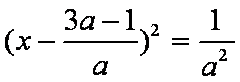

当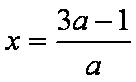
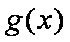
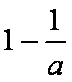
则运动员的飞行距离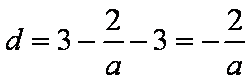
飞行过程中距离平台最大高度
依题意,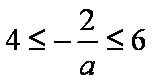

即飞行过程中距离平台最大高度的取值范围为在2米到3米之间,
知识点
扫码查看完整答案与解析