- 抛物线及其性质
- 共383题
已知抛物线的顶点在坐标原点,焦点在

(1)求抛物线的标准方程;
(2)是否存在直线




若存在,求出直线的方程,若不存在,说明理由.
正确答案
见解析
解析
解:(1) 设抛物线方程为
由已知得:
所以抛物线的标准方程为
(2)不存在
因为直线与圆相切, 所以
把直线方程代入抛物线方程并整理得:
由

设












知识点
过抛物线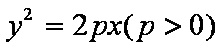
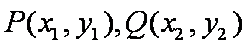
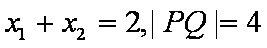
正确答案
解析
由抛物线的定义知: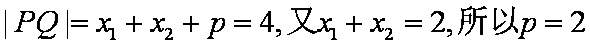
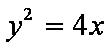
知识点
过抛物线y2=4x的焦点F的直线交该抛物线于A,B两点,若|AF|=3.则|BF|=____ 。
正确答案
解析
易知直线的斜率不存在时,不满足题意;
当直线的斜率存在时,设过抛物线y2=4x的焦点F的直线为






知识点
如图,已知抛物线

(1)求抛物线
(2)过抛物线











正确答案
见解析
解析
(1)

所以

故


(2)任取点


由

由

记


因为

所以
所以
知识点
20.已知抛物线C:y2=2px(p>0)过点A(1,﹣2)。
(Ⅰ)求抛物线C的方程,并求其准线方程;
(Ⅱ)是否存在平行于OA(O为坐标原点)的直线L,使得直线L与抛物线C有公共点,且直线OA与L的距离等于
正确答案
见解析。
解析
(I)将(1,﹣2)代入抛物线方程求得p,则抛物线方程可得,进而根据抛物线的性质求得其准线方程。
(II)先假设存在符合题意的直线,设出其方程,与抛物线方程联立,根据直线与抛物线方程有公共点,求得t的范围,利用直线AO与L的距离,求得t,则直线l的方程可得。
(I)将(1,﹣2)代入抛物线方程y2=2px,
得4=2p,p=2
∴抛物线C的方程为:y2=4x,其准线方程为x=﹣1
(II)假设存在符合题意的直线l,其方程为y=﹣2x+t,
由
∵直线l与抛物线有公共点,
∴△=4+8t≥0,解得t≥﹣
又∵直线OA与L的距离d=

∵t≥﹣
∴t=1
∴符合题意的直线l存在,方程为2x+y﹣1=0
知识点
10.已知抛物线










正确答案
解析
设





知识点
抛物线:







(1) 求抛物线



(2)设点


存在直线



若存在,求直线
正确答案
见解析
解析
解:
(1)抛物线

椭圆

则
(2)设直线




由

故

由





再由


故



由



于是点

由

从而
同理,
若



即

此方程无实根,所以不存在直线



知识点
20.如图,在平面直角坐标系














(1)求抛物线的标准方程;
(2)求证:
(3)若直线


正确答案
见解析。
解析
(1)设抛物线的方程为

所以抛物线的方程为:




由


所以切线AC的方程为:
整理得:
且C点的坐标为
同理得切线BD的方程为:
且D点的坐标为
由(1)(2)消去y,得
又直线AD的方程为:
直线BC的方程为:
由(3)(4)消去y,得


(3)由题意,设

所以
所以直线AB的方程为
知识点
11.已知F是抛物线y2=x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为( )
正确答案
解析
∵F是抛物线y2=x的焦点,
F(

设A(x1,y1),B(x2,y2),
根据抛物线的定义抛物线上的点到焦点的距离等于到准线的距离|AF|=

∴|AF|+|BF|=
解得
∴线段AB的中点横坐标为
∴线段AB的中点到y轴的距离为
故选C.
知识点
9.已知





正确答案
解析
略。
知识点
扫码查看完整答案与解析