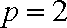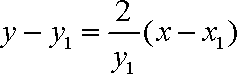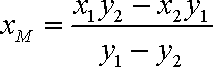- 抛物线及其性质
- 共383题
22.设抛物线C:


(1)求抛物线C的方程;
(2)设点F是抛物线C的焦点,N为抛物线C上的一动点,过N作抛物线C的切线交圆O于P、Q两点,求
正确答案
见解析。
解析
(1)因为抛物线C的准线方程为






(2)设N(



因为圆心O到直线PQ的距离为

设点F到直线PQ的距离为d,则
所以,
当


知识点
6. 已知抛物线C:



正确答案
解析
略
知识点
22.设抛物线C:

(1)求抛物线C的方程;
(2)设点F是抛物线C的焦点,N为抛物线C上的一动点,过N作抛物线C的切线交圆O于P、Q两点,求
正确答案
(1)
解析
(1)因为抛物线C的准线方程为






(2)设N(



因为圆心O到直线PQ的距离为

设点F到直线PQ的距离为d,则
所以,
当


知识点
14. 已知抛物线y2=2px的焦点F与双曲线


正确答案
32
解析
略
知识点
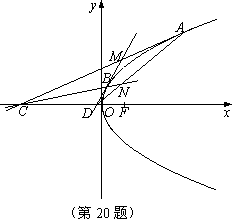
20.如图,在平面直角坐标系
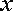
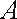
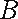
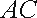
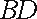
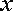


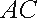
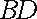
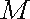


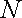
(Ⅰ)求抛物线的标准方程;
(Ⅱ)求证: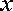
(Ⅲ)若直线
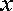
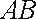
正确答案
见解析。
解析
(1)设抛物线的方程为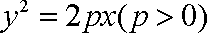
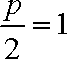
所以抛物线的方程为: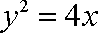

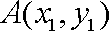
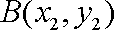
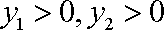
由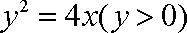
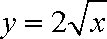
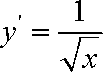
所以切线AC的方程为: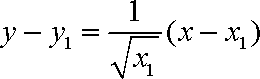
整理得: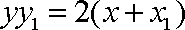
且C点的坐标为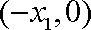
同理得切线BD的方程为: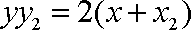
且D点的坐标为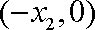
由(1)(2)消去y,得
又直线AD的方程为: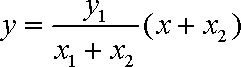
直线BC的方程为: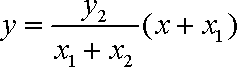
由(3)(4)消去y,得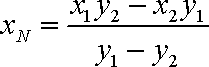
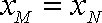
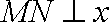
(3)由题意,设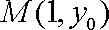
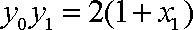
所以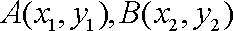
所以直线AB的方程为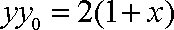
知识点
9.已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.将抛物线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知抛物线y2=2px(p>0)上一点M(1,m)(m>0)到其焦点的距离为5,双曲线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知抛物线



(1)求抛物线的方程;
(2) 设点




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若抛物线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析