抛物线及其性质
共383题

抛物线及其性质
共383题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 16 分

22．抛物线的焦点为圆：的圆心。

（1）求抛物线的方程与其准线方程

（2）直线与圆相切，交抛物线于、两点：

①若线段中点的纵坐标为，求直线的方程

②若直线过抛物线准线与轴的交点，求△的面积。

正确答案

（1）由

得：，

圆心，即。

所以抛物线方程为

准线方程为。

（2）①设：，

由与圆相切得（*）

再由

得

设，

则

由题意：，

得代入（*）得：或

所以直线方程为：

或。

②由题意：直线过，

则，，

所以．在轴同侧

又

当时，，

代入得：

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：简答题

简答题 · 12 分

21．已知抛物线的准线与x轴交点于M.

（1）若M点的坐标为（－1，0），求抛物线方程；

（2）若过点M的直线l与抛物线交P、Q两点，若·（其中F为抛物线的焦点），求直线l的斜率。

正确答案

解：（1）抛物线方程为

（2）设的斜率为k.

设l方程为：

又

代解为：，经检验与抛物线交于两点。

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：填空题

填空题 · 4 分

2．若抛物线的焦点在直线上，则的准线方程为_____。

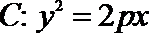
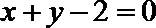
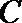
正确答案

x=-2

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：填空题

填空题 · 5 分

13. 抛物线的焦点坐标为________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：单选题

单选题 · 5 分

8. 抛物线上的点到直线距离的最小值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：简答题

简答题 · 12 分

22．抛物线经过点、与，

其中，，设函数在和处取到极值.

（1）用表示；

（2）比较的大小（要求按从小到大排列）；

（3）若，且过原点存在两条互相垂直的直线与曲线均相切，求的解析式.

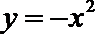
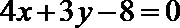
正确答案

（1）由抛物线经过点、设抛物线方程，

又抛物线过点，则，得，

所以。

（2），

，函数在和处取到极值，

故，

，

又，故。

（3）设切点，则切线的斜率

又，所以切线的方程是

又切线过原点，故

所以，解得，或。

两条切线的斜率为，，

由，得，，

，

所以，

又两条切线垂直，故，所以上式等号成立，有，且。

所以。

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：单选题

单选题 · 5 分

12．已知抛物线方程为，直线的方程为，在抛物线上有一动点P到y轴的距离为，P到直线的距离为，则的最小（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：填空题

填空题 · 5 分

15．已知抛物线与椭圆有相同的焦点，是两曲线的一个公共点，若，则此椭圆的离心率为_________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：简答题

简答题 · 13 分

20．已知抛物线的焦点以及椭圆的上、下焦点及左、右顶点均在圆上．

（1）求抛物线和椭圆的标准方程；

（2）过点的直线交抛物线于两不同点，交轴于点，已知，求的值；

（3）直线交椭圆于两不同点，在轴的射影分别为，，若点满足，证明：点在椭圆上．

正确答案

解：（1）由抛物线的焦点在圆上

得：，，∴抛物线

同理由椭圆的上、下焦点及左、右顶点均在圆上

可解得：．得椭圆．

（2）设直线的方程为，则．

联立方程组，消去得：

且

由得：

整理得：

．

（3）设，则

由得；① ；②

；③

由①+②+③得

∴满足椭圆的方程，命题得证．

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：单选题

单选题 · 5 分

10．设、分别为双曲线的左、右焦点，为双曲线的左顶点，以为直径的圆交双曲线某条渐过线、两点，且满足，则该双曲线的离心率为（）

正确答案

解析

不妨设圆与相交且点的坐标为，则点的坐标为，联立，得，，又且，所以由余弦定理得，化简得，求得，故选A.

知识点

抛物线的定义及应用

继续学习学习下一知识点

下一知识点 : 直线与圆锥曲线的位置关系

百度题库 > 高考 > 文科数学 > 抛物线及其性质

扫码查看完整答案与解析