- 函数单调性的性质
- 共384题
在








且
(1) 求角
(2)求
正确答案
见解析。
解析
(1)∵
∴




(2)
又∵


∴
知识点
已知函数

(1)已知函数
(2)若函数

(3)试证明对
正确答案
见解析。
解析
(1)


所以
(2)函数






由




所以a的取值范围为
(3)


知识点
如图,在平面直角坐标系













(1)求直线
(2)求
(3)设










正确答案
见解析。
解析
(1)连结


又

所以


(2)由(1)知,直线



联立解得
因为





由

所以
(3)不妨设

联立方程组

所以
用


同理可得,

所以
因为
当且仅当



知识点
已知函数
(1)求
(2)设


正确答案
见解析。
解析
(1)依题意,有cosx≠0,解得x≠kπ+
即



(2)
由



∴

知识点
经统计,用于数学学习的时间(单位:小时)与成绩(单位:分)近似于线性相关关系。
对某小组学生每周用于数学的学习时间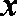
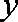
由表中样本数据求得回归方程为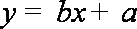
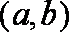
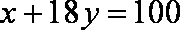
正确答案
解析
样本数据的中心点为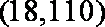
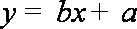
知识点
扫码查看完整答案与解析