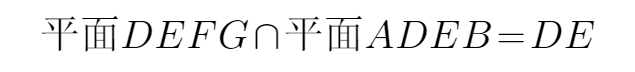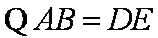- 函数单调性的性质
- 共384题
已知函数

(1)求函数

(2)已知





正确答案
见解析
解析
(1)由题意,


而





所以函数


(2)化简

由正弦定理,得
因为△ABC的外接圆半径为

所以 
知识点
已知




(1)若

(2)试问:是否存在一条平行于

(3)求

正确答案
见解析。
解析
(1)

其交



⊙

(2)∵

∴存在一条平行于


(3)在




∴
∴

故当


知识点
已知函数f(x)=
(1)求y=f(x)在点P(0,1)处的切线方程;
(2)设g(x)=f(x)+x-1仅有一个零点,求实数m的值;
(3)试探究函数f(x)是否存在单调递减区间?若有,设其单调区间为[t,s],试求s-t的取值范围。若没有,请说明理由。
正确答案
见解析
解析
解析:(1)∵点P在函数y=f(x)上,由f(x)=

(2)由g(x)=f(x)+x-1=

则
①当m=1时,

②当m>1时,则
又∵x→-1时,g(x)→-

故此种情况不符题意。………………………………9分
(3)假设y=f(x)存在单调区间,由f(x)=

令


即, 


知识点
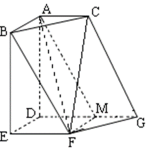
如图,在六面体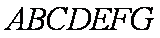
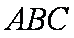
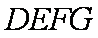
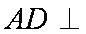
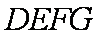

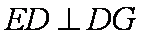
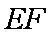
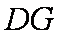
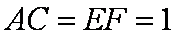
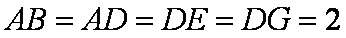
(1)求证:平面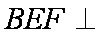
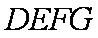
(2)求证: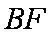
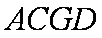
(3)求三棱锥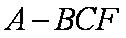
正确答案
见解析。
解析
(1)∵平面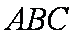
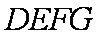

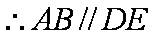
∴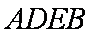
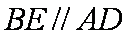
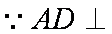
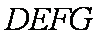
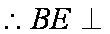

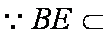
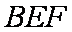
∴平面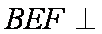
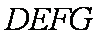
(2)
取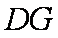
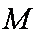
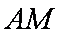
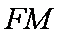
则由已知条件易证四边形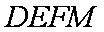
∴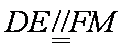
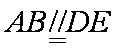
∴四边形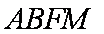
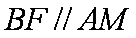
又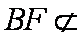
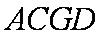
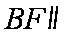
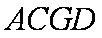
(3)
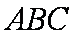
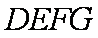
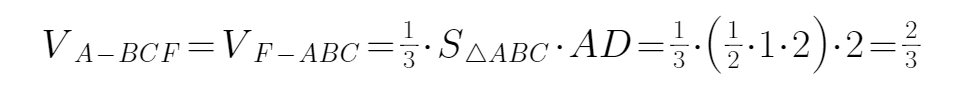
知识点
已知函数f(x)在定义域(0,+∞)上是单调函数,若对任意x∈(0,+∞),都有

正确答案
6
解析
∵函数f(x)在定义域(0,+∞)上是单调函数,且f(f(x)﹣
∴f(x)﹣

再令x=n可得 n+


知识点
扫码查看完整答案与解析