- 函数单调性的性质
- 共384题
如图,在梯形ABCD中,AB//CD,AD=DC=CB=a,

(1)求证:
(2)当EM为何值时,AM//平面BDF?证明你的结论。
正确答案
见解析。
解析
(1)
在梯形




且


又





(2)当


在梯形










又




知识点
如图,矩形




(1)求证: 

(2)求证:平面

正确答案
见解析。
解析
(1)取


又


又


所以

所以






(2)因为平面




因为


又



而



知识点
设M(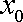
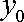
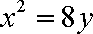
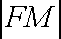
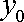
正确答案
解析
由题意只要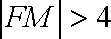
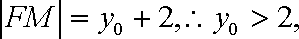
知识点
已知函数
(1)若函数
(2)若


(3)设各项为正数的数列


正确答案
见解析
解析
解析:
(1)函数的定义域为

依题意



当



(2)已知条件等价于方程

设





由
则
(3)先证:当

令








用以上结论,由



所以当

相乘得
又


知识点
已知函数


(1)求
(2)若

正确答案
见解析
解析
(1)由题意,






只须




(2)由(1),得













而

知识点
扫码查看完整答案与解析















