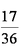- 函数单调性的性质
- 共384题
若关于x的不等式ax>b的解集为

正确答案
解析
∵ ax>b的解集为
∴

∴

所以不等式

即:

知识点
已知平面区域


正确答案
解析
如右图所示,
设直线




∴
扇形
∴阴影部分面积
∴
显然








故答案为:
各自的面积,即可得到

知识点
已知函数




(1)求a,b,c,d的值;
(2)若

正确答案
(1)a=4,b=2,c=2,d=2(2)
解析
解析:(1)由已知得
而
故
(2)令
则
因
令

① 若










故当


② 若









若



综上:

知识点
如图,在平面直角坐标系














(1)求椭圆
(2)证明点
(3)求
正确答案
见解析。
解析
(1)由题意得

解得



(2)设




所以直线

消去


故点

(3)由(2)得点

又


所以点



将


所以






知识点
设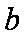
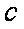
(1)求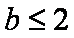
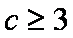
(2)求函数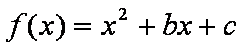
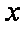
正确答案
(1)P=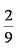
解析
解析:(1)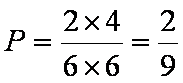
(2)
当

知识点
扫码查看完整答案与解析