- 函数单调性的性质
- 共384题
在






(1)若

(2)若

正确答案
(1)
(2)
解析
(1)解:由正弦定理
得

由于



(2)依题意,


又

另解:
由于


由于

由

由勾股定理

知识点
已知函数



(1)判断曲线


(2)当


正确答案
见解析。
解析
(1)

又


由
由△=
当△>


当△=


当△<

(2)

由

令
当


所以,


因此,
由

所以,当

知识点
函数



正确答案
解析
略
知识点
已知函数
(1)求函数

(2)在
正确答案
见解析。
解析
知识点
已知抛物线
正确答案
解析
略
知识点
对甲、乙两名篮球运动员分别在
(1)估计甲在一场比赛中得分不低于
(2)判断甲、乙两名运动员哪个成绩更稳定;(结论不要求证明)
(3)在甲所进行的100场比赛中,以每场比赛得分所在区间中点的横坐标为这场比赛的得分,试计算甲每场比赛的平均得分。
正确答案
见解析
解析
(1)0.72 ………3分
(2)甲更稳定 ………6分
(3)因为组距为
上得分频率值分别为



设甲的平均得分为
则

知识点
若直线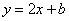
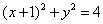
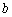
正确答案
解析
略
知识点
下列函数中,既是奇函数又在区间
正确答案
解析
略
知识点
已知向量





(1)求
(2)若


正确答案
见解析。
解析
(1)由题意得
=

令
解得
所以函数

(2) 解法一:因为

又

所以

由正弦定理






所以

所以,

解法二:同上(略)
由余弦定理,



所以,

知识点
已知条件

① 

② 
③ 

④ 
则其中是
正确答案
①③④
解析
略
知识点
扫码查看完整答案与解析

































