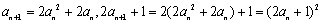- 函数单调性的性质
- 共384题
已知f(x)是定义域为正整数集的函数,对于定义域内任意的k,若f(k)≥k2成立,则f(k+1)≥(k+1)2成立,下列命题成立的是( )
正确答案
解析
由题意对于定义域内任意的k,若f(k)≥k2成立,则f(k+1)≥(k+1)2成立的含义是对前一个数成立,则能推出后一个数成立,反之不成立。
解:对A,当k=1或2时,不一定有f(k)≥k2成立;对B,应有f(k)≥k2成立;
对C,只能得出:对于任意的k≥7,均有f(k)≥k2成立,不能得出:任意的k<7,均有f(k)<k2成立;对D,∵f(4)=25≥16,∴对于任意的k≥4,均有f(k)≥k2成立,故选D
知识点
已知函数f(x)=lnx,
(1)求a,b的值;
(2)求证:当x>1时,f(x)<g(x)成立;
(3)证明:

正确答案
见解析
解析
(1)因为



所以

又因为

由题意
所以

(2)设
则
所以

由



(3)由(2)得,

令

所以

将上述n个不等式依次相加得 
所以
知识点
口袋中装有质地大小完全的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:
甲先摸一个球,记下编号,放回后乙再摸一个球,记下编号.如果两个编号的和为偶数就算甲胜,否则算乙胜.
(1)求甲胜且编号的和为6的事件发生的概率;
(2)这种游戏规则公平吗?说明理由.
正确答案
见解析。
解析
(1)设“甲胜且两个编号的和为6”为事件




所以
答:编号之和为6且甲胜的概率为
(2)这种游戏不公平.
设“甲胜”为事件

所以甲胜的概率为

∵
知识点
点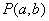
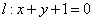
正确答案
解析
略
知识点
若数列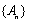
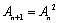
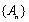
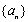
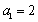
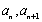
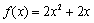
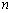
(1)证明数列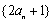
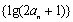
(2)设(1)中“平方递推数列”的前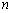
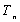
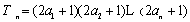
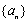
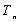
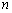
(3)记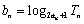
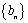
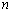
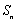
正确答案
见解析
解析
(1)证明:因为
所以数列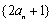
由以上结论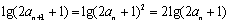
所以数列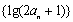
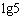
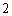
(2)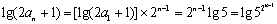
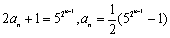
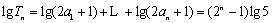
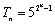
(3)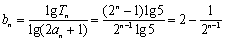
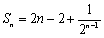
知识点
扫码查看完整答案与解析