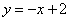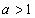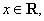- 函数单调性的判断与证明
- 共142题
已知函数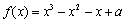
(1)当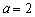
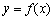
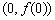
(2)若函数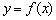
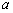
正确答案
(1)
(2)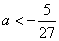
解析
(1)由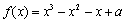
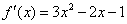
当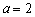
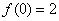
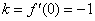
切线方程: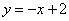
(2)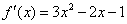
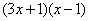
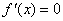
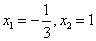
…………6分
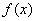
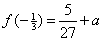
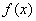
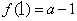
函数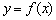
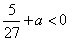
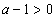
即,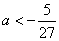
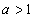
知识点
已知函数
求函数
若函数


正确答案
见解析。
解析
知识点
已知函数

(1)求函数
(2)若函数




正确答案
见解析。
解析
(1)

所以,函数

由







(2)


从而

设

由


知识点
如上左图,目标函数



正确答案
解析
略。
知识点
在约束条件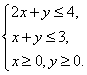
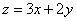
正确答案
7
解析
略
知识点
已知函数
(1)当

(2)若函数
正确答案
见解析。
解析
(1)当
∴
令

当



当



当



∴当

当


(2)∵
∴
① 若

则
函数
② 若



则
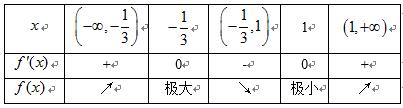
当x变化时,

∵
∴
∴
同理,
∴

令

此时
综上所述,a的取值范围是
知识点
已知函数


正确答案
解析
略
知识点
过点

正确答案
解析
略
知识点
已知函数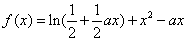
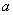
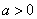
(1)若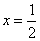
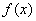
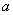
(2)求证:当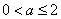
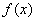
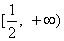
(3)若对任意的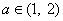
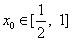
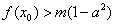
正确答案
见解析。
解析
(1)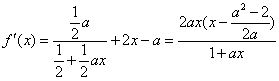
由已知,得 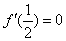
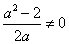
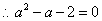
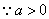
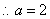
(2)当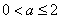
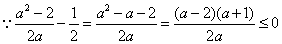
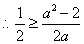

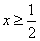
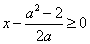
又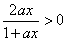
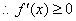
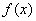
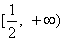
(3)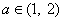
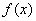
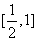
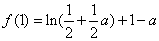
于是问题等价于:对任意的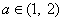
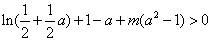
记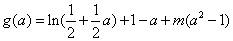
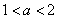
则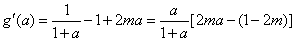
当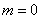
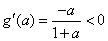
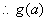
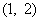
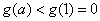
由于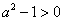
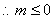
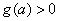
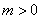
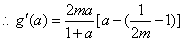
若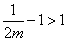
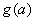
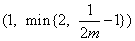
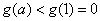
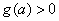
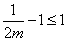
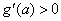
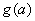
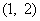
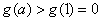
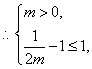
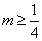
所以,实数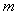
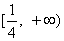
知识点
函数

正确答案
解析
略
知识点
扫码查看完整答案与解析